题目内容
如图1,在平面直角坐标系中,M为x轴正半轴上一点,⊙M与x轴交于A、B两点,与y轴交于点D,P是AB延长线上的一点,过P点作⊙M的切线,切点为C,连接AC,交y轴于点E.若D点的坐标为(0, ),B点的坐标为(3,0).
),B点的坐标为(3,0).

(1)求M点的坐标;
(2)若∠CPA=30°,求CE的长;
(3)在(2)的条件下,若点P在AB的延长线上运动,∠CPA的平分线交AC于点Q.过C、Q、P作⊙N(如图2),弦FQ⊥PQ,试找出线段CQ、FQ、PQ之间的固定的数量关系,并证明.
解:(1)如图1,连接DM,设MD=MC=r,则MO=3-r
在Rt△DOM中,MO2+OD2=MD2,
即 ,
,
解得:r=2,
∴MO=3-r=3-2=1,
∴M(1,0);
(2)如图1,连接MC,由题意:∠MCP=90°
∵∠CPA=30°,
∴∠CMP=60°,
∵MA=MC,
∴∠MAC=∠MCA= ∠CMP=30°,
∠CMP=30°,
∴AC= ,
,
在Rt△AOE中,∠MAC=30°,
∴OE= AE,
AE,
设OE=x,则AE=2x,
在Rt△AOE中,OE2+OA2=AE2,即x2+12=(2x)2
解得: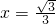 ,
,
∴AE=2x= ,
,
∴CE=AC-AE= ;
;
(3)PQ-FQ= CQ.
CQ.
证明:如图2,过C作CG⊥CQ,交PQ于G,
如图1,∵PQ是∠CPA的平分线,
∴∠CPQ=∠QPA,
∵MA=MC,
∴∠CAM=∠ACM;
在△PCM中,
∵∠CAP+∠ACP+∠CPA=180°,
∴2∠CAM+2∠QPA=90°,∠CAM+∠QPA=45°,
∴∠CQP=∠CAP+∠QPA=45°,
即∠CQP的大小不发生变化为45°,
∵CG⊥CQ,
∴∠QCG=90°,
∴∠CGQ=∠CQG=45°,
∴CQ=CG,QG= QC,
QC,
∵FQ⊥PQ,
∴∠FQP=90°,
∴∠FCP=90°,
∵∠QCF+90°=∠QCG+∠PCG=90°+∠PCG,
∴∠PCG=∠QCF,
在△QCF和△CGP中,
 ,
,
∴△QCF≌△CGP(AAS),
∴QF=PG,
∴PQ-PG=QG,即PQ-FQ= QC.
QC.
分析:(1)利用勾股定理直接求出r,进而得出M点坐标;
(2)首先求出AC的长,再设OE=x,则AE=2x,在Rt△AOE中,OE2+OA2=AE2,得出AE的长即可得出答案;
(3)首先得出∠CQP=45°,进而得出△QCF≌△CGP(AAS),即可得出线段CQ、FQ、PQ之间的固定的数量关系.
点评:此题主要考查了圆的综合应用以及全等三角形的判定与性质和角平分线的性质等知识,利用已知得出∠CQP的大小不发生变化为45°进而得出CQ=CG是解题关键.
在Rt△DOM中,MO2+OD2=MD2,
即
 ,
,解得:r=2,
∴MO=3-r=3-2=1,
∴M(1,0);
(2)如图1,连接MC,由题意:∠MCP=90°
∵∠CPA=30°,
∴∠CMP=60°,
∵MA=MC,
∴∠MAC=∠MCA=
 ∠CMP=30°,
∠CMP=30°,∴AC=
 ,
,在Rt△AOE中,∠MAC=30°,
∴OE=
 AE,
AE,设OE=x,则AE=2x,
在Rt△AOE中,OE2+OA2=AE2,即x2+12=(2x)2
解得:
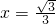 ,
,∴AE=2x=
 ,
,∴CE=AC-AE=
 ;
;(3)PQ-FQ=
 CQ.
CQ.证明:如图2,过C作CG⊥CQ,交PQ于G,
如图1,∵PQ是∠CPA的平分线,
∴∠CPQ=∠QPA,
∵MA=MC,
∴∠CAM=∠ACM;
在△PCM中,
∵∠CAP+∠ACP+∠CPA=180°,
∴2∠CAM+2∠QPA=90°,∠CAM+∠QPA=45°,
∴∠CQP=∠CAP+∠QPA=45°,
即∠CQP的大小不发生变化为45°,
∵CG⊥CQ,
∴∠QCG=90°,
∴∠CGQ=∠CQG=45°,
∴CQ=CG,QG=
 QC,
QC,
∵FQ⊥PQ,
∴∠FQP=90°,
∴∠FCP=90°,
∵∠QCF+90°=∠QCG+∠PCG=90°+∠PCG,
∴∠PCG=∠QCF,
在△QCF和△CGP中,
 ,
,∴△QCF≌△CGP(AAS),
∴QF=PG,
∴PQ-PG=QG,即PQ-FQ=
 QC.
QC.分析:(1)利用勾股定理直接求出r,进而得出M点坐标;
(2)首先求出AC的长,再设OE=x,则AE=2x,在Rt△AOE中,OE2+OA2=AE2,得出AE的长即可得出答案;
(3)首先得出∠CQP=45°,进而得出△QCF≌△CGP(AAS),即可得出线段CQ、FQ、PQ之间的固定的数量关系.
点评:此题主要考查了圆的综合应用以及全等三角形的判定与性质和角平分线的性质等知识,利用已知得出∠CQP的大小不发生变化为45°进而得出CQ=CG是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;
23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′; 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为

 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 再绕着点
再绕着点 点,这时点
点,这时点 与点
与点 为旋转中心时,点
为旋转中心时,点 点,点
点,点 点,点
点,点 点,小明发现P、
点,小明发现P、 两点关于点
两点关于点 中心对称.
中心对称.


 、
、 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到点
旋转180°得到点 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点 ,则点
,则点 的坐为.
的坐为. ,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),
,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),