题目内容
用“▲”“●”“◆”分别表示三种物体的重量,若 ,那么▲,●,◆这三种物体的重量比为
,那么▲,●,◆这三种物体的重量比为
- A.2:3:4
- B.2:4:3
- C.3:4:5
- D.3:5:4
B
分析:可设 =k,利用等比性质可得用k的值,进而用各分母表示出各分子的值得到3个等式,联立可得“▲”“●”“◆”用▲表示其他物体的重量,相比即可.
=k,利用等比性质可得用k的值,进而用各分母表示出各分子的值得到3个等式,联立可得“▲”“●”“◆”用▲表示其他物体的重量,相比即可.
解答:设 =k,
=k,
则▲为x,●为y,◆为z.
k= =
= =
=
∴x= y;y-z=
y;y-z= x;z=
x;z= (x+y),
(x+y),
∴y=2x,z= x;
x;
∴▲,●,◆这三种物体的重量比为x:2x: x=2:4:3,
x=2:4:3,
故选B.
点评:考查比例性质的应用;利用等比性质得到所给比值的确定值是解决本题的难点.
分析:可设
 =k,利用等比性质可得用k的值,进而用各分母表示出各分子的值得到3个等式,联立可得“▲”“●”“◆”用▲表示其他物体的重量,相比即可.
=k,利用等比性质可得用k的值,进而用各分母表示出各分子的值得到3个等式,联立可得“▲”“●”“◆”用▲表示其他物体的重量,相比即可.解答:设
 =k,
=k,则▲为x,●为y,◆为z.
k=
 =
= =
=
∴x=
 y;y-z=
y;y-z= x;z=
x;z= (x+y),
(x+y),∴y=2x,z=
 x;
x;∴▲,●,◆这三种物体的重量比为x:2x:
 x=2:4:3,
x=2:4:3,故选B.
点评:考查比例性质的应用;利用等比性质得到所给比值的确定值是解决本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 答下列问题:
答下列问题: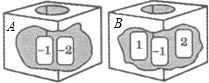 的卡片,它们分别写有数字1,-1,2.现从A箱、B箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
的卡片,它们分别写有数字1,-1,2.现从A箱、B箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求: