题目内容
 如图,?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F.
如图,?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F.(1)请直接写出两组相等的线段;
(2)若△FDE的周长为9,△FCB的周长为23,求?ABCD的周长.
分析:(1)根据翻折变换的性质可知,△ABE≌△FBE,由全等三角形的对应边相等即可解答;
(2)根据△ABE≌△FBE,可知EA=EF,AB=FB,再由△FDE的周长为9,△FCB的周长为23即可求解.
(2)根据△ABE≌△FBE,可知EA=EF,AB=FB,再由△FDE的周长为9,△FCB的周长为23即可求解.
解答:解:(1)由翻折变换的性质可知,△ABE≌△FBE,
故AB=DC,AD=BC,AE=EF,AB=BF,CD=BF等任写两组;(2分)
(2)依题意,得:△ABE≌△FBE(3分)
∴EA=EF,AB=FB(4分)
∵
(5分)
∴DE+EA+DF=9FC+BC+AB=23(6分)
∴DE+EA+DF+FC+BC+AB=32(7分)
∴AD+DC+BC+AB=32
∴?ABCD的周长为32.(8分)
故答案为:AB=DC,AD=BC,32.
故AB=DC,AD=BC,AE=EF,AB=BF,CD=BF等任写两组;(2分)
(2)依题意,得:△ABE≌△FBE(3分)
∴EA=EF,AB=FB(4分)
∵
|
∴DE+EA+DF=9FC+BC+AB=23(6分)
∴DE+EA+DF+FC+BC+AB=32(7分)
∴AD+DC+BC+AB=32
∴?ABCD的周长为32.(8分)
故答案为:AB=DC,AD=BC,32.
点评:本题考查的是图形翻折变换的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
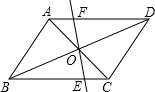 如图,?ABCD中,AB⊥AC,AB=1,BC=
如图,?ABCD中,AB⊥AC,AB=1,BC=| 5 |
| A、当旋转角为90°时,四边形ABEF一定为平行四边形 |
| B、在旋转的过程中,线段AF与EC总相等 |
| C、当旋转角为45°时,四边形BEDF一定为菱形 |
| D、当旋转角为45°时,四边形ABEF一定为等腰梯形 |
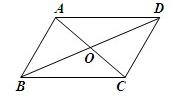 9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )
9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )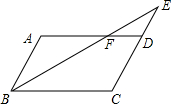 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=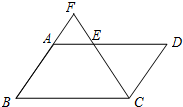 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F. (1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为
(1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为