��Ŀ����
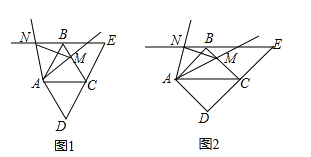
����Ŀ�� ��2016����Ӫ�ڵ�25�⣩��֪����ͼ�٣�����D=60�������ABCD�ضԽ���AC����������ADC������DC����ƽ�ƣ��õ���BCE����MΪ��BC��һ�㣨��M�����B����C�غϣ���������AM�Ƶ�A��ʱ����ת60�㣬��EB���ӳ��߽��ڵ�N������MN��
��1������֤����ANB=��AMC��
��̽����AMN����״��
��2����ͼ�ڣ�������ABCD��Ϊ������ABCD��������AM�Ƶ�A��ʱ����ת45�㣬ԭ�������������䣬��1���еĢ١������������Ƿ���Ȼ����������������ֱ��д�����ۣ�������������д���仯��Ľ��۲�֤����

���𰸡���1����֤�����������ڡ�AMN�ǵȱ�����������2���ٳ������ڲ���������AMN�ǵ���ֱ�������Σ�
��������
�����������1�����������ο�֪�ı���ȣ�������D=60��õȱ���ADC�͵ȱ���ABC����Խ���AC���ı߶���ȣ�����ASA֤����ANB�ա�AMC���ý��ۣ�
�ڸ�����һ������60��ĵ����������ǵȱ������εó�����AMN�ǵȱ������Σ�
��2���ٳ��������������ε�45��Ǻ�����AM�Ƶ�A��ʱ����ת45�㣬֤����ANB�ס�AMC������ANB=��AMC��
�ڲ���������AMN�ǵ���ֱ�������Σ����â��е���ANB�ס�AMC���ñ���ʽ���б��κ���֤����NAM�ס�BAD������AMN�ǵ���ֱ�������Σ�
�����������1����ͼ1�������ı���ABCD�����Σ���AB=BC=CD=AD���ߡ�D=60�㣬���ADC����ABC�ǵȱ������Σ���AB=AC����BAC=60�㣬�ߡ�NAM=60�㣬���NAB=��CAM������ADC������DC����ƽ�Ƶõ���BCE����֪��CBE=60�㣬�ߡ�ABC=60�㣬���ABN=60�㣬���ABN=��ACB=60�㣬���ANB�ա�AMC�����ANB=��AMC��
����ͼ1����AMN�ǵȱ������Σ������ǣ�
����ANB�ա�AMC����AM=AN���ߡ�NAM=60�㣬���AMN�ǵȱ������Σ�
��2������ͼ2����ANB=��AMC�����������ǣ�
��������ABCD�У����BAC=��DAC=��BCA=45�㣬�ߡ�NAM=45�㣬���NAB=��MAC����ƽ�Ƶã���EBC=��CAD=45�㣬�ߡ�ABC=90�㣬���ABN=180�㩁90�㩁45��=45�㣬���ABN=��ACM=45�㣬���ANB�ס�AMC�����ANB=��AMC��
����ͼ2������������AMN�ǵ���ֱ�������Σ������ǣ�
�ߡ�ANB�ס�AMC����![]() ����
����![]() ���ߡ�NAM=��BAC=45�㣬���NAM�ס�BAC�����ANM=��ABC=90�㣬���AMN�ǵ���ֱ�������Σ�
���ߡ�NAM=��BAC=45�㣬���NAM�ס�BAC�����ANM=��ABC=90�㣬���AMN�ǵ���ֱ�������Σ�

 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�


