题目内容
若x+y+z=1,且x,y,z∈R,则x2+y2+z2与
的大小关系为 .
【解析】x2+y2+z2-=(3x2+3y2+3z2-1)
=[3x2+3y2+3z2-(x+y+z)2]
=[(x-y)2+
(y-z)2+(z-x)2]≥0
即x2+y2+z2≥.
答案:x2+y2+z2≥
练习册系列答案
阅读快车系列答案
相关题目
若a为实数，且a≠0，则下列各式中一定成立的是（ ）
| A、a2+1＞1 | ||
| B、1-a2＜0 | ||
C、1+
| ||
D、1-
|
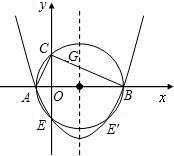如图，在Rt△ABC中，∠ACB=90°，BC＞AC，以斜边AB所在直线为x轴，以斜边AB上的高所在直线为y轴，建立直角坐标系，若OA2+OB2=17，且线段OA、OB的长度是关于x的一元二次方程x2-mx+2（m-3）=0的两个根．若a+b=-2，且a≥2b，则（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（2012•泰州模拟）如图，已知反比例函数