题目内容
如图，将矩形纸片ABCD沿EF折叠（E、F分别是AD、BC上的点），使点B与四边形CDEF内一点B′重合，若∠B′FC=50°，则∠AEF等于
- A.110°
- B.115°
- C.120°
- D.130°
B
分析：先根据平角的性质及折叠的性质可求出∠EFB′的度数，再根据平行线的性质解答即可．
解答：∵四边形A′EFB′是四边形ABFE折叠而成，
∴∠BFE=∠EFB′，
∵∠B'FC=50°，
∴∠EFB=
=
=65°，
∵AD∥BC，
∴∠AEF=180°-∠EFB=115°．
故选B．
点评：本题考查的是折叠的性质及平行线的性质：
（1）折叠的性质：图形折叠后与原图形完全重合；
（2）平行线的性质：两直线平行，同旁内角互补．
分析：先根据平角的性质及折叠的性质可求出∠EFB′的度数，再根据平行线的性质解答即可．
解答：∵四边形A′EFB′是四边形ABFE折叠而成，
∴∠BFE=∠EFB′，
∵∠B'FC=50°，
∴∠EFB=
==65°，∵AD∥BC，
∴∠AEF=180°-∠EFB=115°．
故选B．
点评：本题考查的是折叠的性质及平行线的性质：
（1）折叠的性质：图形折叠后与原图形完全重合；
（2）平行线的性质：两直线平行，同旁内角互补．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
23、如图，将矩形纸片ABCD沿EF折叠，使点A与点C重合，点D落在点G处，EF为折痕．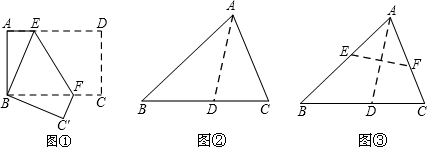
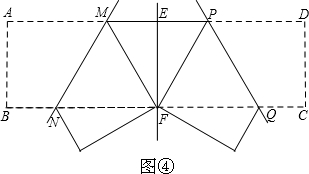
（2013•松北区三模）如图，将矩形纸片ABCD折痕，使点D落在点线段AB的中点F处．若AB=4，则边BC的长为（ ）
如图，将矩形纸片ABCD沿其对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E．
