题目内容
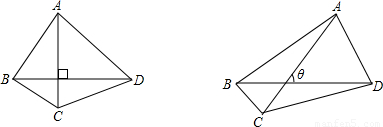
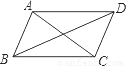
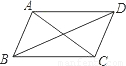
(2008•泰安)四边形ABCD的对角线AC、BD的长分别为m、n,可以证明当AC⊥BD时(如左图),四边形ABCD的面积S= mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)
mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)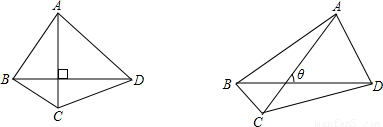
【答案】分析:设AC、BD交于O点,在①图形中,设BD=m,OA+OC=n,所以S四边形ABCD=S△ABD+S△BDC,由此可以求出四边形的面积;
在②图形中,作AE⊥BD于E,CF⊥BD于F,由于AC、BD夹角为θ,所以AE=OA•sinθ,CF=OC•sinθ,∴S四边形ABCD=S△ABD+S△BDC= BD•AE+
BD•AE+ BD•CF=
BD•CF= BD•(AE+CF ),由此也可以求出面积.
BD•(AE+CF ),由此也可以求出面积.
解答:解:如图,设AC、BD交于O点,在①图形中,设BD=m,OA+OC=n,
所以S四边形ABCD=S△ABD+S△BDC= m•OC+
m•OC+ m•OA=
m•OA= mn;
mn;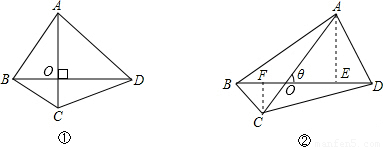
在②图形中,作AE⊥BD于E,CF⊥BD于F,
由于AC、BD夹角为θ,
所以AE=OA•sinθ,CF=OC•sinθ,
∴S四边形ABCD=S△ABD+S△BDC
= BD•AE+
BD•AE+ BD•CF
BD•CF
= BD•(AE+CF)=
BD•(AE+CF)= mnsinθ.
mnsinθ.
故填空答案: mnsinθ.
mnsinθ.
点评:此题比较难,解题时关键要找对思路,即原四边形的高已经发生了变化,只要把高求出来,一切将迎刃而解.
在②图形中,作AE⊥BD于E,CF⊥BD于F,由于AC、BD夹角为θ,所以AE=OA•sinθ,CF=OC•sinθ,∴S四边形ABCD=S△ABD+S△BDC=
 BD•AE+
BD•AE+ BD•CF=
BD•CF= BD•(AE+CF ),由此也可以求出面积.
BD•(AE+CF ),由此也可以求出面积.解答:解:如图,设AC、BD交于O点,在①图形中,设BD=m,OA+OC=n,
所以S四边形ABCD=S△ABD+S△BDC=
 m•OC+
m•OC+ m•OA=
m•OA= mn;
mn;
在②图形中,作AE⊥BD于E,CF⊥BD于F,
由于AC、BD夹角为θ,
所以AE=OA•sinθ,CF=OC•sinθ,
∴S四边形ABCD=S△ABD+S△BDC
=
 BD•AE+
BD•AE+ BD•CF
BD•CF=
 BD•(AE+CF)=
BD•(AE+CF)= mnsinθ.
mnsinθ.故填空答案:
 mnsinθ.
mnsinθ.点评:此题比较难,解题时关键要找对思路,即原四边形的高已经发生了变化,只要把高求出来,一切将迎刃而解.

练习册系列答案
相关题目
 mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)
mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)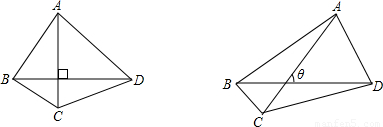
 mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)
mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)