题目内容
 如图,已知AB=4,DB⊥AB,EA⊥AB,DB=3,EA=6,又点M是DE的中点,求BM的长.
如图,已知AB=4,DB⊥AB,EA⊥AB,DB=3,EA=6,又点M是DE的中点,求BM的长.
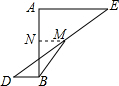 解:过M作MN⊥AB于N点,如图,
解:过M作MN⊥AB于N点,如图,∵点M是DE的中点,DB⊥AB,EA⊥AB,
∴AE∥MN∥DB,NB=
 AB=
AB= ×4=2,
×4=2,∴MN=
 (AE-BD),
(AE-BD),而DB=3,EA=6,
∴MN=
 ,
,在Rt△BMN中,BM2=BN2+MN2=22+(
 )2=
)2= ,
,∴BM=
 .
.分析:过M作MN⊥AB于N点,由点M是DE的中点,DB⊥AB,EA⊥AB,得到AE∥MN∥DB,NB=
 AB=
AB= ×4=2,则MN=
×4=2,则MN= (AE-BD)=
(AE-BD)= ,
,在Rt△BMN中,利用勾股定理即可计算出BM.
点评:本题考查了平行于三角形一边的直线与其它两边所得的三角形与原三角形相似.也考查了三角形的中位线性质以及勾股定理.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 24、如图,已知AB=AC,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由.
24、如图,已知AB=AC,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由. 17、(保留作图痕迹)如图,已知AB=DC.
17、(保留作图痕迹)如图,已知AB=DC.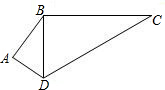 如图,已知AB=4,BC=12,CD=13,DA=3,AB⊥AD.判断BC⊥BD吗?简述你的理由.
如图,已知AB=4,BC=12,CD=13,DA=3,AB⊥AD.判断BC⊥BD吗?简述你的理由. 如图:已知AB∥DE,点C是AE的中点,
如图:已知AB∥DE,点C是AE的中点, 如图,已知AB、CD交于点O,且点O是AB的中点,AC∥BD,请说明点O是CD的中点的理由.
如图,已知AB、CD交于点O,且点O是AB的中点,AC∥BD,请说明点O是CD的中点的理由.