题目内容
如图，扇形DOE的半径为3，边长为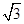
的菱形OABC的顶点A，C，B分别在OD，OE，
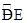上，若把扇形DOE围成一个圆锥，则此圆锥的高为【 】
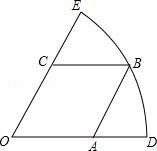
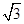的菱形OABC的顶点A，C，B分别在OD，OE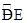，上，若把扇形DOE围成一个圆锥，则此圆锥的高为【 】A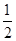． | B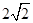． | C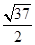． | D． |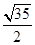
D
连接OB，AC，BO与AC相交于点F。
∵在菱形OABC中，AC⊥BO，CF=AF，FO=BF，∠COB=∠BOA，
又∵扇形DOE的半径为3，边长为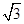，∴FO=BF=1.5。cos∠FOC=
。
∴∠FOC=30°。∴∠EOD=2×30°=60°。∴
。
底面圆的周长为：2πr=π，解得：r=。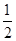
∵圆锥母线为：3，∴此圆锥的高为：
。故选D
∵在菱形OABC中，AC⊥BO，CF=AF，FO=BF，∠COB=∠BOA，
又∵扇形DOE的半径为3，边长为
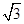，∴FO=BF=1.5。cos∠FOC=。∴∠FOC=30°。∴∠EOD=2×30°=60°。∴
。底面圆的周长为：2πr=π，解得：r=
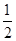。∵圆锥母线为：3，∴此圆锥的高为：
。故选D
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
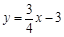交x轴、y轴于点A、B，⊙P的圆心从原点出发以每秒1个单位的速度向x轴正方向移动，移动时间为t(s)，半径为
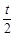，则t = s时⊙P与直线AB相切．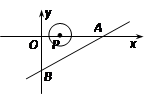
，则
的长等于
B.
C. 
D.
弧AE=弧BE ； ④2CE·AB=BC2，
、⊙
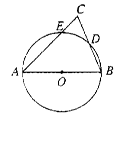
相内切于点A，其半径分别是8和4，将⊙
，点M是⊙O上的动点，且使