题目内容
如图,已知△ABC中,∠BAC=36°,AB=AC=2,动点D在CB的延长线上运动,动点E在BC的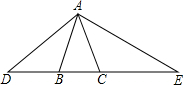 延长线上运动,且保持∠DAE的值为108°.设DB=x,CE=y.
延长线上运动,且保持∠DAE的值为108°.设DB=x,CE=y.(1)求y与x之间的函数关系式;
(2)用描点法画出(1)中函数的图象;
(3)已知直线y=x-3与(1)中函数图象的交点坐标是(a,b),求
| a |
| b |
| b |
| a |
(4)求BC的长.
分析:(1)根据题意可知∠D=∠CAE,∠DAB=∠E,推出△DAB∽△AEC,即可求出y与x的之间的函数表达式;
(2)首先画出表格,在描点,连线即可;
(3)把交点坐标代入两个解析式,即可得出关于a和b方程组,求解即可;
(4)作∠ABC的平分线BF交AC于点F,结合题意,可推出AF=BF=BC,△CBF∽△CAB,即得BC2=AC•CF.推出AF2=AC•CF,求出AF后即可得BC的长度.
(2)首先画出表格,在描点,连线即可;
(3)把交点坐标代入两个解析式,即可得出关于a和b方程组,求解即可;
(4)作∠ABC的平分线BF交AC于点F,结合题意,可推出AF=BF=BC,△CBF∽△CAB,即得BC2=AC•CF.推出AF2=AC•CF,求出AF后即可得BC的长度.
解答:解:(1)AB=AC,∠BAC=36°,∠DAE=108°.
∴∠ABC=∠ACB=
=72°,∠DAB+∠CAE=72°.
∴∠D+∠DAB=72°,∠CAE+∠E=72°.
∴∠D=∠CAE,∠DAB=∠E.
∴△DAB∽△AEC.
∴
=
.
∴
=
(x>0).
∴y=
(x>0)
(2)完成表格,描点绘图

(3)根据题意,得
,
∴ab=4,a-b=3.
∴
+
=
=
=
=
;
(4)作∠ABC的平分线BF交AC于点F.
∵∠ABC=∠ACB=72°,
∴∠ABF=∠FBC=36°.
∴∠BFC=72°.
∴AF=BF=BC.
在△CBF和△CAB中,
∵∠BCF=∠ACB,∠CBF=∠CBA,
∴△CBF∽△CAB.
∴
=
.
∴BC2=AC•CF.
∴AF2=AC•CF.
∴AF=
•AC=
-1.
∴BC=
-1.
∴∠ABC=∠ACB=
| 180°-36° |
| 2 |
∴∠D+∠DAB=72°,∠CAE+∠E=72°.
∴∠D=∠CAE,∠DAB=∠E.
∴△DAB∽△AEC.
∴
| DB |
| AC |
| AB |
| EC |
∴
| x |
| 2 |
| 2 |
| y |
∴y=
| 4 |
| x |
(2)完成表格,描点绘图
| x | 1 | 2 | 4 | 5 | 8 | 10 |
| y | 4 | 2 | 1 | 0.8 | 0.5 | 0.4 |

(3)根据题意,得
|
∴ab=4,a-b=3.
∴
| b |
| a |
| a |
| b |
| b2+a2 |
| ab |
| (a-b)2+2ab |
| ab |
| 32+2×4 |
| 4 |
| 17 |
| 4 |
(4)作∠ABC的平分线BF交AC于点F.

∵∠ABC=∠ACB=72°,
∴∠ABF=∠FBC=36°.
∴∠BFC=72°.
∴AF=BF=BC.
在△CBF和△CAB中,
∵∠BCF=∠ACB,∠CBF=∠CBA,
∴△CBF∽△CAB.
∴
| CF |
| BC |
| BC |
| AC |
∴BC2=AC•CF.
∴AF2=AC•CF.
∴AF=
| ||
| 2 |
| 5 |
∴BC=
| 5 |
点评:本题主要考查相似三角形的判定和性质、反比例函数的图象、反比例函数与一次函数交点的问题,解题的关键在于求出三角形相似和有关的函数图象.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.
如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.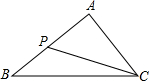 如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( )
如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( ) (2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( )
(2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( ) 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( ) 如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )
如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )