题目内容
△ABC中∠A为锐角,cosA=| 3 | 5 |
(1)求y关于x的函数解析式和自变量x的取值范围;
(2)当AC长度为何值时,△ABC的面积最大,最大面积是多少?
分析:(1)可根据AB,AC的关系,先表示出AB,而sinA其实就是AB边上的高与AC边的比.因此也可用AC表示出三角形的高,那么根据三角形的面积公式即可得出关于x、y的函数关系式;
(2)根据(1)得出的函数解析式以及自变量的取值范围即可得出面积的最大值以及此时AC的长度.
(2)根据(1)得出的函数解析式以及自变量的取值范围即可得出面积的最大值以及此时AC的长度.
解答: 解:(1)由题意可知:AB=6-x(cm),sinA=
解:(1)由题意可知:AB=6-x(cm),sinA=
,
那么y=
×AB×CD=
×AB×AC•sinA=
×(6-x)×
x=-
x2+
x,
即:y=-
x2+
x(0<x<6);
(2)由(1)可知:y=-
x2+
x=-
(x-3)2+
,
因此当x=3时,ymax=
,
即当AC=3cm,三角形ABC的面积最大,最大值是
cm2.
 解:(1)由题意可知:AB=6-x(cm),sinA=
解:(1)由题意可知:AB=6-x(cm),sinA=| 4 |
| 5 |
那么y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 12 |
| 5 |
即:y=-
| 2 |
| 5 |
| 12 |
| 5 |
(2)由(1)可知:y=-
| 2 |
| 5 |
| 12 |
| 5 |
| 2 |
| 5 |
| 18 |
| 5 |
因此当x=3时,ymax=
| 18 |
| 5 |
即当AC=3cm,三角形ABC的面积最大,最大值是
| 18 |
| 5 |
点评:本题主要考查了二次函数的应用,求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
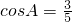 ,AB+AC=6(cm),设AC=xcm,△ABC的面积为ycm2.
,AB+AC=6(cm),设AC=xcm,△ABC的面积为ycm2. ,AB+AC=6(cm),设AC=xcm,△ABC的面积为ycm2.
,AB+AC=6(cm),设AC=xcm,△ABC的面积为ycm2. ,AB+AC=6(cm),设AC=xcm,△ABC的面积为ycm2.
,AB+AC=6(cm),设AC=xcm,△ABC的面积为ycm2.