题目内容
17.经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在下列横线上:
销售单价x(元)x;
销售量y(件)1000-10x;
销售玩具获得利润w(元)-10x2+1300x-30000;
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
分析 (1)销售量=600-减少的数量,利润=每件的获利×销售量;
(2)依据商场获得了10000元销售利润列出关于x的方程求解即可;
(3)接下来,依据销售单价不低于44元,且商场要完成不少于540件的销售任务列不等式组求解即可.
解答 解:(1)销售单价(元)x,销售量y=600-10(x-40)=1000-10x,
销售玩具获得利润w(元)=(x-30)(1000-10x)=-10x2+1300x-30000.
故答案为:x;1000-10x;-10x2+1300x-30000.
(2)-10x2+1300x-30000=10000
解之得:x1=50,x2=80
答:玩具销售单价为50元或80元时,可获得10000元销售利润.
(3)根据题意得$\left\{\begin{array}{l}{1000-10≥540}\\{x≥44}\end{array}\right.$
解之得:44≤x≤46,
w=-10x2+1300x-30000=-10(x-65)2+12250,
∵a=-10<0,对称轴是直线x=65,
∴当44≤x≤46时,w随x增大而增大.
∴当x=46时,W最大值=8640(元).
答:商场销售该品牌玩具获得的最大利润为8640元.
点评 本题主要考查的是二次函数的应用,依据题意列出函数关系式是解题的关键.

练习册系列答案
相关题目
8.如果|a-1|+(b+2)2=0,则(a+b)2016的值是( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
12.已知点P(-3,1)关于原点对称的点的坐标是( )
| A. | (1,3) | B. | (3,-1) | C. | (-3,-1) | D. | (-1,3) |
9.方程x2-22x+2=0的根的情况为( )
| A. | 有一个实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 有两个相等的实数根 |
6.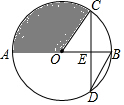 如图,AB是⊙O的直径,弦CD⊥AB于点E,且E为OB的中点,CD=4$\sqrt{3}$,则图中阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,且E为OB的中点,CD=4$\sqrt{3}$,则图中阴影部分的面积为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,且E为OB的中点,CD=4$\sqrt{3}$,则图中阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,且E为OB的中点,CD=4$\sqrt{3}$,则图中阴影部分的面积为( )| A. | π | B. | 4π | C. | $\frac{4}{3}$π | D. | $\frac{16}{3}$π |
7. 实数b在数轴上的位置如图所示,则实数b可能的取值为( )
实数b在数轴上的位置如图所示,则实数b可能的取值为( )
 实数b在数轴上的位置如图所示,则实数b可能的取值为( )
实数b在数轴上的位置如图所示,则实数b可能的取值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{7}$-2 |