题目内容
已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m-5,2).
(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90º?若存在,求出m的取值范围;若不存在,请说明理由.
(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.
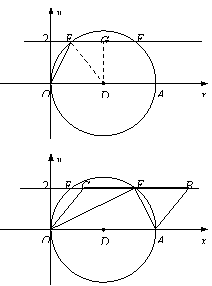 解:(1)由题意,知:BC∥OA.以OA为直径作⊙D,与直
解:(1)由题意,知:BC∥OA.以OA为直径作⊙D,与直
线BC分别交于点E、F,则∠OEA=∠OFA=90º.
作DG⊥EF于G,连DE,则DE=OD=2.5,DG=2,
EG=GF,∴ EG=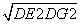 =1.5,
=1.5,
∴点E(1,2),点F(4,2).
∴当 即1≤m≤9时,边BC上总存在这样的点P,
即1≤m≤9时,边BC上总存在这样的点P,
使∠OPA=90º.
(2)∵BC=5=OA,BC∥OA,∴四边形OABC是平行四边形.
当Q在边BC上时,∠OQA =180º-∠QOA-∠QAO
=180º- (∠COA+∠OAB)=90º,∴点Q只能是点E或点F
(∠COA+∠OAB)=90º,∴点Q只能是点E或点F .
.
当Q在F点时,∵OF、AF分别是∠AOC与∠OAB的平分
线,BC∥OA,∴∠CFO=∠FOA=∠FOC,∠BFA=∠FAO=
∠FAB,∴CF=OC,BF=AB,∵OC=AB,∴F是BC的中
点.∵F点为 (4,2),∴此时m的值为6.5.
当Q在E点时,同理可求得此时m的值为3.5.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目


 B.
B.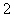 C.
C. D.
D.
 C. π D. -8
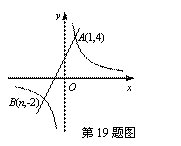
C. π D. -8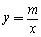 的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).