题目内容
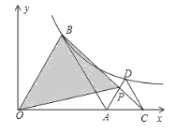
【题目】如图,在平面直角坐标系中,已知点A(5,3),点B(﹣3,3),过点A的直线y=![]() x+m(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D.
x+m(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D.
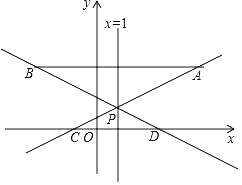
(1)求点P的坐标;
(2)求直线BP的解析式,并直接写出△PCD与△PAB的面积比;
(3)若反比例函数![]() (k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值.
(k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值.
【答案】(1)P(1,1); (2)![]() ;(3)当k<0时,最小值为-9;当k>0时,最大值为
;(3)当k<0时,最小值为-9;当k>0时,最大值为![]()
【解析】
试题![]() 把点
把点![]() 坐标代入一次函数
坐标代入一次函数![]() ,求得
,求得![]() 的值,进而求得点
的值,进而求得点![]() 的坐标.
的坐标.
![]() 用待定系数法即可求得直线
用待定系数法即可求得直线![]() 的解析式,直接计算面积即可求出它们的比值.
的解析式,直接计算面积即可求出它们的比值.
![]() 分成
分成![]() 和
和![]() 两种情况进行讨论.
两种情况进行讨论.
试题解析:(1)∵![]() 过点A(5,3),
过点A(5,3),
![]()
解得:![]()
∴y=![]() ,
,
当![]() 时,∴
时,∴![]() ,
,
∴![]()
(2)设直线BP的解析式为y=ax+b,
根据题意,得![]()
解得: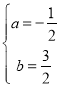
∴直线BP的解析式为![]() ,
,
点![]()
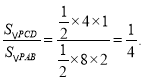
(3)当![]() 时,经过点
时,经过点![]() 时,有最小值为-9;
时,有最小值为-9;
当![]() 时,联立方程
时,联立方程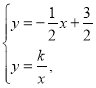 整理得,
整理得,![]()
![]() 解得:
解得:![]()
即最大值为![]() .
.

【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段,下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
跳远(米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
跳绳(次) | 63 |
| 75 | 60 | 63 | 72 | 70 |
|
| 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则( )
A.5号学生进入30秒跳绳决赛
B.2号学生进入30秒跳绳决赛
C.8号学生进入30秒跳绳决赛
D.9号学生进入30秒跳绳决赛
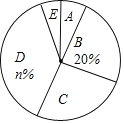
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 | A | B | C | D | E |
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 12 | 30 | m | 54 | 9 |
请你根据以上的信息,回答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %.
(2)被调查学生的总数为 人,统计表中m的值为 ,统计图中n的值为 .
(3)在统计图中,E类所对应扇形圆心角的度数为 .
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱新闻节目的学生数.