��Ŀ����
��֪���κ���y=x2-mx+m-2����1����֤������mΪ�κ�ʵ�����ö��κ�����ͼ����x�ᶼ���������㣻
��2�����ö��κ�����ͼ���㣨3��6��ʱ������κ����Ľ���ʽ��
��3����ֱ��y=x����ƽ��2����λ���Ⱥ��루2���е������߽���A��B���㣨��A�ڵ�B����ߣ���һ������P��A��������ȵ��������ߵĶԳ����ϵ�ij��E���ٵ���x���ϵ�ij��F������˶�����B����ʹ��P�˶�����·����̵ĵ�E����F�����꣬�������������·���ij���
���𰸡���������1�������ߵĽ���ʽ�У���y=0������������x�����������㣬��ô���÷��̵ĸ����б�ʽ����0���ɾݴ���֤������Ľ��ۣ�
��2������֪��������������������߽���ʽ�У������������ϵ��m��ֵ���Ӷ�ȷ���������ߵĽ���ʽ��
��3��ֱ��y=x����ƽ��2����λ����ʽΪ��y=x-2���ϼ��¼��������������ߵĽ���ʽ������õ�A��B�����ꣻ��P���˶������·����Ҳ������AE+EF+BF����Сֵ����ȡA���������߶Գ���ĶԳƵ�A�䣬ȡB����x��ĶԳƵ�B�䣬A�䡢B�����������ã����ɵõ�ֱ��A��B��Ľ���ʽ����ôֱ��A��B���������߶Գ����x��Ľ��㣬��Ϊ�����E��F�㣬��ʱP���˶������·����ΪA��B��ij�������A�䡢B�������������߶�A��B��ij����ɴ˵ý⣮
��� ��1��֤������y=0����x2-mx+m-2=0��
��1��֤������y=0����x2-mx+m-2=0��
�ߡ�=��-m��2-4��m-2��=m2-4m+8=��m-2��2+4����1�֣�
�֡ߣ�m-2��2��0��
�ࣨm-2��2+4��0��������0��
������mΪ�κ�ʵ����һԪ���η���x2-mx+m-2=0����������ʵ����
��ö��κ���ͼ����x�ᶼ���������㣮��2�֣�
��2���⣺�߶��κ���y=x2-mx+m-2��ͼ���㣨3��6����
��32-3m+m-2=6��
���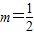 ��
��
����κ����Ľ���ʽΪ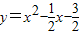 ����3�֣�
����3�֣�
��3���⣺��y=x����ƽ��2����λ���Ⱥ�õ�����ʽΪ��y=x-2����4�֣�
�ⷽ����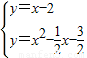 ��
��
��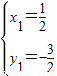 ��
��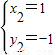 ��
��
��ֱ��y=x-2��������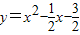 �Ľ���Ϊ
�Ľ���Ϊ ��
��
���A���ڶԳ���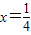 �ĶԳƵ���
�ĶԳƵ���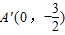 ��
��
��B����x��ĶԳƵ���B'��1��1���������A'��B'��ֱ�߽���ʽΪy=kx+b��
��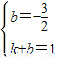 ��
��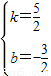 ��
��
��ֱ��A'B'�Ľ���ʽΪ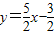 ��
��
��ֱ��A'B'��x��Ľ���Ϊ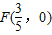 ��5�֣�
��5�֣�
��ֱ��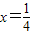 �Ľ���Ϊ
�Ľ���Ϊ ��6�֣�
��6�֣�
���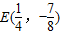 ��
��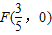 ����
����
����B'��B'H��AA'���ӳ����ڵ�H��
��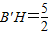 ��HA'=1��
��HA'=1��
��Rt��A'B'H��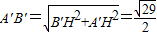 ��
��
�����������·���ij�ΪAE+EF+FB=A'B'=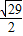 ����7�֣�
����7�֣�
�����������Ƕ��κ������ۺ��⣬�����˸����б�ʽ����������ʽ��ȷ��������ͼ�����������ԳƵ����ʡ�ƽ��չ��-���·���������Ҫ֪ʶ�㣬�ۺ���ǿ���ѶȽϴ�
��2������֪��������������������߽���ʽ�У������������ϵ��m��ֵ���Ӷ�ȷ���������ߵĽ���ʽ��
��3��ֱ��y=x����ƽ��2����λ����ʽΪ��y=x-2���ϼ��¼��������������ߵĽ���ʽ������õ�A��B�����ꣻ��P���˶������·����Ҳ������AE+EF+BF����Сֵ����ȡA���������߶Գ���ĶԳƵ�A�䣬ȡB����x��ĶԳƵ�B�䣬A�䡢B�����������ã����ɵõ�ֱ��A��B��Ľ���ʽ����ôֱ��A��B���������߶Գ����x��Ľ��㣬��Ϊ�����E��F�㣬��ʱP���˶������·����ΪA��B��ij�������A�䡢B�������������߶�A��B��ij����ɴ˵ý⣮
���
 ��1��֤������y=0����x2-mx+m-2=0��
��1��֤������y=0����x2-mx+m-2=0���ߡ�=��-m��2-4��m-2��=m2-4m+8=��m-2��2+4����1�֣�
�֡ߣ�m-2��2��0��
�ࣨm-2��2+4��0��������0��
������mΪ�κ�ʵ����һԪ���η���x2-mx+m-2=0����������ʵ����
��ö��κ���ͼ����x�ᶼ���������㣮��2�֣�
��2���⣺�߶��κ���y=x2-mx+m-2��ͼ���㣨3��6����
��32-3m+m-2=6��
���
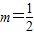 ��
������κ����Ľ���ʽΪ
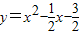 ����3�֣�
����3�֣���3���⣺��y=x����ƽ��2����λ���Ⱥ�õ�����ʽΪ��y=x-2����4�֣�
�ⷽ����
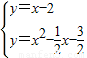 ��
����
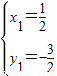 ��
��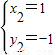 ��
����ֱ��y=x-2��������
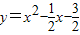 �Ľ���Ϊ
�Ľ���Ϊ ��
�����A���ڶԳ���
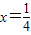 �ĶԳƵ���
�ĶԳƵ���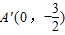 ��
����B����x��ĶԳƵ���B'��1��1���������A'��B'��ֱ�߽���ʽΪy=kx+b��
��
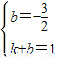 ��
��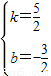 ��
����ֱ��A'B'�Ľ���ʽΪ
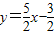 ��
����ֱ��A'B'��x��Ľ���Ϊ
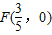 ��5�֣�
��5�֣���ֱ��
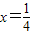 �Ľ���Ϊ
�Ľ���Ϊ ��6�֣�
��6�֣����
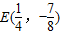 ��
��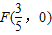 ����
Ϊ��������B'��B'H��AA'���ӳ����ڵ�H��
��
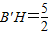 ��HA'=1��
��HA'=1����Rt��A'B'H��
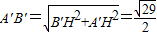 ��
�������������·���ij�ΪAE+EF+FB=A'B'=
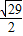 ����7�֣�
����7�֣������������Ƕ��κ������ۺ��⣬�����˸����б�ʽ����������ʽ��ȷ��������ͼ�����������ԳƵ����ʡ�ƽ��չ��-���·���������Ҫ֪ʶ�㣬�ۺ���ǿ���ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
��֪���κ���y=x2+��2a+1��x+a2-1����СֵΪ0����a��ֵ�ǣ�������
A��
| ||
B��-
| ||
C��
| ||
D��-
|
 ��֪���κ���y=-x2+2x+m�IJ���ͼ����ͼ��ʾ�������x��һԪ���η���-x2+2x+m=0�Ľ�Ϊ��������
��֪���κ���y=-x2+2x+m�IJ���ͼ����ͼ��ʾ�������x��һԪ���η���-x2+2x+m=0�Ľ�Ϊ��������| A��x1=1��x2=3 | B��x1=0��x2=3 | C��x1=-1��x2=1 | D��x1=-1��x2=3 |
 ��֪���κ���y=-x2+bx+c��ͼ����ͼ��ʾ������x���һ����������Ϊ��-1��0������y��Ľ�������Ϊ��0��3����
��֪���κ���y=-x2+bx+c��ͼ����ͼ��ʾ������x���һ����������Ϊ��-1��0������y��Ľ�������Ϊ��0��3����