��Ŀ����
����Ŀ���Ķ������
���������е�![]() ������
������![]() ���������ڵ��������������ұߵ�����ȥ��ߵ���������֮��д����������֮�䣬�ɲ���һ����������
���������ڵ��������������ұߵ�����ȥ��ߵ���������֮��д����������֮�䣬�ɲ���һ���������� ![]() ���Ϊ��һ�β������ڶ���ͬ���IJ�����Ҳ�ɲ���һ����������
���Ϊ��һ�β������ڶ���ͬ���IJ�����Ҳ�ɲ���һ����������![]() �������β�����ȥ����
�������β�����ȥ����
![]() �������ſ���
�������ſ���![]() ������
������ ![]() ����һ�β��������ӵ���������֮���Ƕ���?
����һ�β��������ӵ���������֮���Ƕ���?
![]() ��
��![]() ��ǰ���£������ڶ��β��������õ��������ȵ�һ�β��������õ��������ӵ���������֮���Ƕ���?
��ǰ���£������ڶ��β��������õ��������ȵ�һ�β��������õ��������ӵ���������֮���Ƕ���?
![]() ���룺�������ſ���
���룺�������ſ���![]() ������
������![]() ��һ�ٴβ�����õ����������ȵھ�ʮ�Ŵβ��������õ��������ӵ���������֮���Ƕ���?
��һ�ٴβ�����õ����������ȵھ�ʮ�Ŵβ��������õ��������ӵ���������֮���Ƕ���?
���𰸡���1��4����2��4����3��![]() .
.
��������
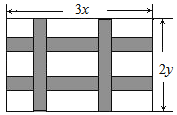
��1���������������ĵ�һ�β�����ģʽ����ʱ�����������Բ������ɣ�
��2�����ݣ�1����֪��һ�β������������Ϊ��![]() ���ݴ˽�һ�����еڶ��β������ɵó��ڶ��β��������������Ȼ���һ�����㼴�ɣ�
���ݴ˽�һ�����еڶ��β������ɵó��ڶ��β��������������Ȼ���һ�����㼴�ɣ�
��3�����������������һ�β��������õ������������ӵ�����֮�ͣ�Ȼ����ݣ�1������2���еĽ��������ǰ���һ���ڶ��������εIJ��������õ������������ӵ�����֮�Ͳ�û�з����仯���ݴ˽�һ�����뼴��.
��1��������ÿɵã�
��![]() ��һ�β��������õ�������Ϊ��
��һ�β��������õ�������Ϊ��![]() ��
��
�������ӵ�����Ϊ��![]() ��
��
��![]() ��
��
����һ�β��������ӵ���������֮����4��
��2���ɣ�1���ɵõ�һ�β������������Ϊ��![]() ��
��
��ڶ��β������������Ϊ��![]() ��
��
�������ӵ�����Ϊ��![]() ��
��
��![]() ��
��
���ڶ��β��������õ��������ȵ�һ�β��������õ��������ӵ���������֮��Ϊ4��
��3��������ã�![]() ��һ�β�����ɵ�������Ϊ��
��һ�β�����ɵ�������Ϊ��![]() ��
��
��ʱ�����ӵ���Ϊ��![]() ��
��
��![]() ��
��
���ڶ��β��������õ��������ȵ�һ�β��������õ��������ӵ���������֮��Ϊ![]() ��
��
���ݣ�1������2���Ĵ𰸿��Է��֣���ǰ���һ���ڶ��εIJ��������õ������������ӵ�����֮�Ͳ�û�з����仯��
�� ���뷲��ǰ���������ڲ��������õ������������ӵ�����֮�Ͳ��ᷢ���仯��
��![]() ��һ�ٴβ�����õ����������ȵھ�ʮ�Ŵβ��������õ��������ӵ���������֮��Ϊ��
��һ�ٴβ�����õ����������ȵھ�ʮ�Ŵβ��������õ��������ӵ���������֮��Ϊ��![]() .
.