题目内容
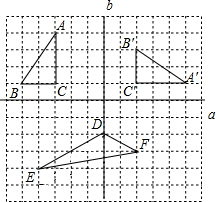
 在如图所示的4×4的方格中,每个小正方形的边长都为1.
在如图所示的4×4的方格中,每个小正方形的边长都为1.(1)请在图中画出一个三角形,使它的三条边长分别为3,2
| 2 |
| 5 |
(2)所画三角形的面积是
分析:(1)由于每个小正方形的边长为1,所以作△ABC,由勾股定理确定AB、BC、AC即可;
(2)如下图所示该三角形的面积等于四边形的面积减去另外两个三角形的面积.
(2)如下图所示该三角形的面积等于四边形的面积减去另外两个三角形的面积.
解答:解:(1)所要做的图如下所示:

由于每个小正方形的边长为1,由勾股定理得:
AB=
=
,BC=
=2
,AC=3.
(2)所画三角形的面积为:S△ABC=3×2-
×2×1-
×2×2=3.

由于每个小正方形的边长为1,由勾股定理得:
AB=
| 22+12 |
| 5 |
| 22+22 |
| 2 |
(2)所画三角形的面积为:S△ABC=3×2-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查勾股定理的应用,通过勾股定理确定三角形的各个边长,并在4×4的方格中作出图形,并利用图形的特殊位置求面积.

练习册系列答案
相关题目
 在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”根据图形,解决下面的问题:
在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”根据图形,解决下面的问题: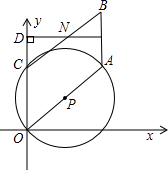 A、B两点不重合),点N是DM与BC的交点,设OD=t;
A、B两点不重合),点N是DM与BC的交点,设OD=t; 动到终点时,两个动点都停止运动.
动到终点时,两个动点都停止运动.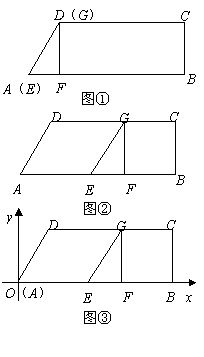 如图
如图
