Question

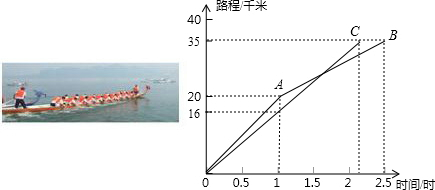
第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕．20日上午9时，参赛龙舟从黄陵庙同时出发．其中甲、乙两队在比赛时，路程y（千米）与时间x（小时）的函数关系如图所示．甲队在上午11时30分到达终点黄柏河港．在比赛过程中，甲、乙两队在出发后    小时相距最远．

Answer 1

【答案】分析：根据甲队达到的时间确定出O-A-B是甲队的图象，OC是乙队的图象，然后根据函数图象求出在点A时与在点C是两队的距离，进行比较即可求出两队相距最远的距离以及时间．
解答：解：∵上午9时参赛龙舟同时出发，甲队在上午11时30分到达终点，
∴O-A-B是甲队的图象，
则OC是乙队的图象，
由图可知，出发后甲队速度较快，乙队速度较慢，当出发1小时后甲乙两队相距20-16=4千米，
1小时后，甲队速度放慢，乙队速度不变，然后相遇直至最后分别到达终点，
AB段，函数图象经过点（1，20）（2.5，35），
设直线AB解析式为y=kx+b，
则，
解得，
所以，y=10x+10，
直线OC经过点（0，0）（1，16），
所以直线OC解析式为y=16x，
16x=35，
x=，
所以点C的坐标为（，35），
此时甲乙两队相距：35-（×10+10）=25-=，
∵4＞，
∴甲、乙两队在出发后1小时相距最远，最远距离是4．
故答案为：1．
点评：本题考查了一次函数的应用，根据图象求出在点A与点C两点时的两队相距的距离是解题的关键，本题还利用了待定系数法求函数解析式．