题目内容
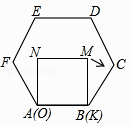
【题目】如图，在平面直角坐标系中，
坐标分别是
，且
满足
，现同时将点分别向下平移3个单位，再向左平移1个单位，分别得到点的对应点
，连接
．
（1）求点的坐标及四边形
的面积
；
（2）在y轴上是否存在一点
，连接
，使
？若存在这样的点，求出点M的坐标，若不存在，试说明理由．
【答案】（1）
（2）在
轴上存在点
，或
使
【解析】
（1）由偶次方及绝对值的非负性可求出a、b的值，进而即可得出点A、B的坐标，再根据平移的性质可得出点C、D的坐标；根据坐标与图形的性质求出四边形ABCD的面积；
（2）设M坐标为（0，），根据三角形的面积公式列出方程，解方程求出，得到点M的坐标；
解：（1）依题意得：
解得：
，
将点
分别向下平移3个单位，再向左平移1个单位，
（2）假设在轴上存在点
，使
,
，
，
或
所以在轴上存在点，使.
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
