题目内容
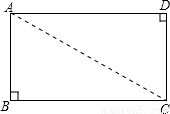
 如图,矩形纸片ABCD中,AB=8cm.把矩形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=
如图,矩形纸片ABCD中,AB=8cm.把矩形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,若AF=| 25 | 4 |
分析:由折叠的性质可证AF=FC.在Rt△ADF中,由勾股定理求AD的长.
解答:解:由折叠的性质知,AE=CD,CE=AD,
∴△ADC≌△CEA,∠EAC=∠DCA,
∴AF=CF=
cm,DF=CD-CF=
,
在Rt△ADF中,由勾股定理得,
AD2=AF2-DF2,则AD=6cm.
故答案为:6.
∴△ADC≌△CEA,∠EAC=∠DCA,
∴AF=CF=
| 25 |
| 4 |
| 7 |
| 4 |
在Rt△ADF中,由勾股定理得,
AD2=AF2-DF2,则AD=6cm.
故答案为:6.
点评:本题考查了翻折变换的知识,其中利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②全等三角形的判定和性质,勾股定理求解.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4
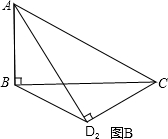

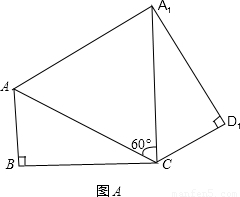
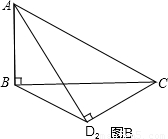
 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E. ,将矩形沿对角线AC剪开,解答以下问题:
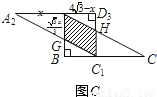
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



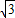 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: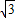 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.