Question

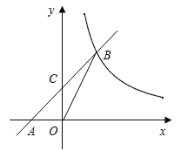
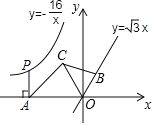
【题目】如图，点P是反比例函数图象上的一动点，轴于点A，在直线上截取点B在第一象限，点C的坐标为，连接AC、BC、OC．

填空：______，______；

求证：∽；

随着点P的运动，的大小是否会发生变化？若变化，请说明理由，若不变，则求出它的大小．

Answer 1

【答案】（1）4；（2）证明见解析（3）120°

【解析】

（1）过点C作CE⊥x轴于点E，过点B作BF⊥x轴于点F，由点C的坐标可得出OE，CE的长度，进而可求出OC的长度及∠AOC的度数，由直线OB的解析式可得出∠BOF的度数，再利用∠BOC=180°﹣∠AOC﹣∠BOF即可求出∠BOC的度数；

（2）由（1）可知∠AOC=∠BOC，由点P是反比例函数y（x＜0）图象上的一动点，利用反比例函数图象上点的坐标特征可得出PAOA=16，结合OB=PA及OC=4，可得出，结合∠AOC=∠BOC即可证出△AOC∽△COB；

（3）由△AOC∽△COB利用相似三角形的性质可得出∠CAO=∠BCO．在△AOC中，利用三角形内角和定理可求出∠CAO+∠OCA=120°，进而可得出∠BCO+∠OCA=120°，即∠ACB=120°．

（1）过点C作CE⊥x轴于点E，过点B作BF⊥x轴于点F，如图所示．

∵点C的坐标为（﹣2，2），∴OE=2，CE=2，∴OC4．

∵tan∠AOC，∴∠AOC=60°．

∵直线OB的解析式为yx，∴∠BOF=60°，∴∠BOC=180°﹣∠AOC﹣∠BOF=60°．

故答案为：4；60°．

（2）∵∠AOC=60°，∠BOC=60°，∴∠AOC=∠BOC．

∵点P是反比例函数y（x＜0）图象上的一动点，∴PAOA=16．

∵PA=OB，∴OBOA=16=OC2，即，∴△AOC∽△COB．

（3）∠ACB=120°，不会发生变化．理由如下：

∵△AOC∽△COB，∴∠CAO=∠BCO．

在△AOC中，∠AOC=60°，∴∠CAO+∠OCA=120°，∴∠BCO+∠OCA=120°，即∠ACB=120°．