题目内容
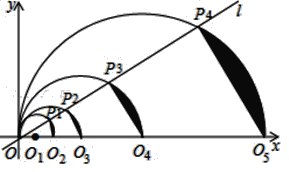
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=![]() x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和
x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画半圆,交直线l于点P1,交x轴正半轴于点O2,由弦P1O2和![]() 围成的弓形面积记为S1,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围
围成的弓形面积记为S1,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,由弦P2O3和围![]() 成的弓形面积记为S2,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和
成的弓形面积记为S2,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4,由弦P3O4和![]() 围成的弓形面积记为S3;…按此做法进行下去,其中S2018的面积为__________.
围成的弓形面积记为S3;…按此做法进行下去,其中S2018的面积为__________.
【答案】![]()
【解析】
连接P1O1,根据直线的函数解析式与特殊角的三角函数值得到∠P1OO1=30°,则∠P1O1O2=60°,再根据扇形面积公式与等边三角形的面积公式求得S1,S2,S3,S4找到规律,然后求解S2018即可.
解:如图,连接P1O1,
∵直线l的函数表达式为y=![]() x,
x,
∴tan P1OO1=![]() ,
,
∴∠P1OO1=30°,
∴∠P1O1O2=60°,
则S1=![]() ﹣
﹣![]() =
=![]() ,
,
同理可得S2=![]() ,
,
S3=![]() ,
,
S4=![]() =
=![]() ,
,
······
Sn=![]() ,
,
则当n=2018时,
S2018=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目