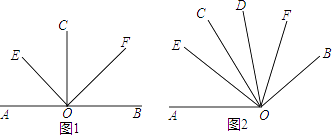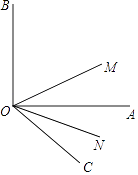��Ŀ����
����Ŀ����ͼ����֪AM��BN����A=60�㣮��P������AM��һ���㣨���A���غϣ���BC��BD�ֱ�ƽ�֡�ABP�͡�PBN���ֱ�����AM�ڵ�C��D�� 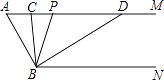
��1���١�ABN�Ķ������� �ڡ�AM��BN�����ACB=����
��2�����CBD�Ķ�����
��3������P�˶�ʱ����APB���ADB֮���������ϵ�Ƿ���֮�����仯�������仯����д������֮��Ĺ�ϵ����˵�����ɣ����仯����д���仯���ɣ�
��4������P�˶���ʹ��ACB=��ABDʱ����ABC�Ķ����� ��
���𰸡�
��1��120�㣻CBN
��2���⣺��AM��BN��
���ABN+��A=180�㣬
���ABN=180�㩁60��=120�㣬
���ABP+��PBN=120�㣬
��BCƽ�֡�ABP��BDƽ�֡�PBN��
���ABP=2��CBP����PBN=2��DBP��
��2��CBP+2��DBP=120�㣬
���CBD=��CBP+��DBP=60��
��3���⣺���䣬��APB����ADB=2��1��
��AM��BN��
���APB=��PBN����ADB=��DBN��
��BDƽ�֡�PBN��
���PBN=2��DBN��
���APB����ADB=2��1
��4��30��
���������⣺��1���١�AM��BN����A=60�㣬 ���A+��ABN=180�㣬
���ABN=120�㣻�ڡ�AM��BN��
���ACB=��CBN��
�ʴ�Ϊ��120�㣬��CBN����4����AM��BN��
���ACB=��CBN��
����ACB=��ABDʱ�����С�CBN=��ABD��
���ABC+��CBD=��CBD+��DBN��
���ABC=��DBN��
�ɣ�1����֪��ABN=120�㣬��CBD=60�㣬
���ABC+��DBN=60�㣬
���ABC=30�㣬
�ʴ�Ϊ��30�㣮
��1����ƽ���ߵ����ʣ���ֱ��ƽ��ͬ���ڽǻ������ڴ�����ȿɵã���2���ɣ�1��֪��ABP+��PBN=120�㣬�ٸ��ݽ�ƽ���ߵĶ���֪��ABP=2��CBP����PBN=2��DBP���ɵ�2��CBP+2��DBP=120�㣬����CBD=��CBP+��DBP=60�㣻��3����AM��BN�á�APB=��PBN����ADB=��DBN������BDƽ�֡�PBN֪��PBN=2��DBN���Ӷ��ɵá�APB����ADB=2��1����4����AM��BN�á�ACB=��CBN������ACB=��ABDʱ�С�CBN=��ABD���á�ABC+��CBD=��CBD+��DBN������ABC=��DBN�����ݡ�ABN=120�㣬��CBD=60��ɵô𰸣�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�