题目内容
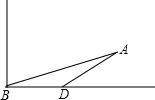
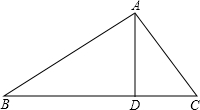
如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长(答案可带根号).


作AB⊥CD交CD的延长线于点B,
在Rt△ABC中,
∵∠ACB=∠CAE=30°,∠ADB=∠EAD=45°,
∴AC=2AB,DB=AB.
设AB=x,则BD=x,AC=2x,CB=50+x,
∵tan∠ACB=tan30°,
∴AB=CB•tan∠ACB=CB•tan30°.
∴x=(50+x)•
.
解得:x=25(1+
),
∴AC=50(1+
)(米).
答:缆绳AC的长为50(1+
)米.

在Rt△ABC中,
∵∠ACB=∠CAE=30°,∠ADB=∠EAD=45°,
∴AC=2AB,DB=AB.
设AB=x,则BD=x,AC=2x,CB=50+x,
∵tan∠ACB=tan30°,
∴AB=CB•tan∠ACB=CB•tan30°.
∴x=(50+x)•
| ||
| 3 |
解得:x=25(1+
| 3 |
∴AC=50(1+
| 3 |
答:缆绳AC的长为50(1+
| 3 |


练习册系列答案
相关题目