题目内容
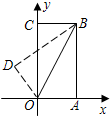 如图,平面直角坐标系中,已知矩形OABC,O为原点,点A、C分别在x轴、y轴上,点B的坐标为(1,2),连接OB,将△OAB沿直线OB翻折,点A落在点D的位置.则点D的坐标为________.
如图,平面直角坐标系中,已知矩形OABC,O为原点,点A、C分别在x轴、y轴上,点B的坐标为(1,2),连接OB,将△OAB沿直线OB翻折,点A落在点D的位置.则点D的坐标为________.
(- ,
, )
)
分析:根据翻折不变性及勾股定理求出GD、CG的长,再根据相似三角形的性质,求出DF的长,进而求出D点坐标.
解答: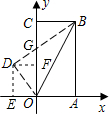 解:作DF⊥y轴于F,DE⊥x轴于E,
解:作DF⊥y轴于F,DE⊥x轴于E,
∵在△BCG与△ODG中,
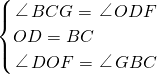
∴△BCG≌△ODG,
∴GO=GB,
∴设GO=GB=x,
则CG=GD=2-x,
于是在Rt△CGB中,(2-x)2+12=x2;
解得x= .
.
GD=2-x=2- =
= ;
;
∵△CBG∽△FDG,
∴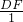 =
=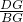 ,
,
∴DF=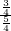 =
= ;
;
又∵DO=1,
∴OF=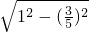 =
= .
.
∴点D的坐标为(- ,
, ).
).
故答案为:(- ,
, ).
).
点评:此题将翻折变换与相似三角形和勾股定理相结合,考查了三角形与矩形的性质,有一定难度,是一道好题.
 ,
, )
)分析:根据翻折不变性及勾股定理求出GD、CG的长,再根据相似三角形的性质,求出DF的长,进而求出D点坐标.
解答:
 解:作DF⊥y轴于F,DE⊥x轴于E,
解:作DF⊥y轴于F,DE⊥x轴于E,∵在△BCG与△ODG中,
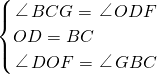
∴△BCG≌△ODG,
∴GO=GB,
∴设GO=GB=x,
则CG=GD=2-x,
于是在Rt△CGB中,(2-x)2+12=x2;
解得x=
 .
.GD=2-x=2-
 =
= ;
;∵△CBG∽△FDG,
∴
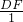 =
=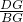 ,
,∴DF=
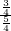 =
= ;
;又∵DO=1,
∴OF=
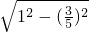 =
= .
.∴点D的坐标为(-
 ,
, ).
).故答案为:(-
 ,
, ).
).点评:此题将翻折变换与相似三角形和勾股定理相结合,考查了三角形与矩形的性质,有一定难度,是一道好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.