题目内容
如图，已知：DE∥BC，且AD=DF=FB，AE=EG=GC，则S△ADE：S四边形DFGE：S四边形FBCG是
- A.1：2：3
- B.1：2：4
- C.1：3：5
- D.1：4：9
C
分析：根据DE∥FG∥BC，得到△ADE∽△AFG∽△ABC，然后用相似三角形面积的比等于相似比的平方可以求出它们的比值．
解答：∵DE∥FG∥BC，
∴△ADE∽△AFG∽△ABC，
∵AD=DF=FB，
∴S△ADE：S△AFG：S△ABC=1：4：9．
∴S△ADE：S四边形DFGE：S四边形FBCG=1：3：5．
故选C．
点评：本题考查的是相似三角形的判定与性质，根据线段平行判定三角形相似，再用相似三角形的性质得到对应边的比和面积的比，然后求出它们的比值．
分析：根据DE∥FG∥BC，得到△ADE∽△AFG∽△ABC，然后用相似三角形面积的比等于相似比的平方可以求出它们的比值．
解答：∵DE∥FG∥BC，
∴△ADE∽△AFG∽△ABC，
∵AD=DF=FB，
∴S△ADE：S△AFG：S△ABC=1：4：9．
∴S△ADE：S四边形DFGE：S四边形FBCG=1：3：5．
故选C．
点评：本题考查的是相似三角形的判定与性质，根据线段平行判定三角形相似，再用相似三角形的性质得到对应边的比和面积的比，然后求出它们的比值．
练习册系列答案
53随堂测系列答案
相关题目
如图，已知AB∥DE，AB=DE，AF=DC，求证：四边形BCEF是平行四边形．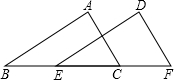
如图，已知AB=DE，AC=DF，要使△ABC≌△DEF，还需要补充一个条件，你补充的条件是：
如图，已知：DE∥BC，AD：DB=1：2，DE=2，则BC=（ ）
如图，已知AB∥DE，BC∥EF，D，C在AF上，且AD=CF，请补充完整过程，说明△ABC≌△DEF的理由．
如图，已知AC∥DE，∠1=∠2．求证：AB∥CD．