Question

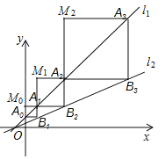
【题目】在平面直角坐标系中，点A是直线上一点，点B是轴上一点，且AB=6，则△AOB面积的最大值是________．

Answer 1

【答案】

【解析】

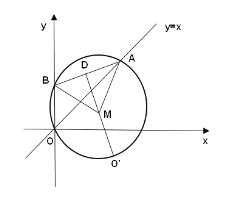
设三角形ABO的外接圆为⊙M，假设AB不动，当点O运动到点O’时候，△AOB的面积最大，根据题中条件求出O’D的大小，即可求得△AOB面积的最大值.

设三角形ABO的外接圆为⊙M，过点M作O’D⊥AB于点D，交⊙M于点O’，

假设AB不动，当点O运动到点O’时候，△AOB的面积最大，

根据题意，AB=6，O’D⊥AB

∴AD=BD=3，

∵∠AOB=45°，

∴∠AMB=90°.

∵AM、BM为⊙M的半径，

∴AM=BM=，

DM=

∴O’D=O’M+DM=3+

S△AO’B=AB×O’D=×6×（3+）=

∴△AOB面积的最大值为，

故答案为.