Question

【题目】如图，在等边三角形ABC中，点D、点E分别为AB，AC上的点，BE与CD相交于点F，BF=4EF=4，CE=AD．则S△AEB= ．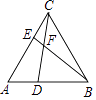

Answer 1

【答案】5
【解析】解：∵△ABC为等边三角形， ∴∠A=∠BCE=60°，AC=CB，
在△ACD和△CBE中， ，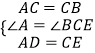
∴△ACD≌△CBE（SAS），
∴∠ACD=CBE．
又∵∠CEF=BEC，
∴△AEF∽△BEC，
∴ ，
∵BF=4EF=4，
∴EC= ．
过点E作EM⊥BC于点M，EN⊥AB于点N，如图所示．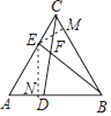

在Rt△AEM中，CE= ，∠ECM=60°，
∴CM= CE= ，EM= CE= ．
在Rt△BME中，BE=5，EM= ，
∴BM= = ．
∴BC=AB=AC= ，AE=AC﹣CE= ，
∴S△AEB= ABEN= × × × =5 ．
故答案为：5 ．
根据等边三角形的性质结合CE=AD，即可得出△ACD≌△CBE（SAS），进而得出∠ACD=CBE，结合∠CEF=BEC，可得出△AEF∽△BEC，根据相似三角形的性质结合BF=4EF=4，即可求出CE的长度，过点E作EM⊥BC于点M，EN⊥AB于点N，通过解直角三角形可求出BC的长度，再根据三角形的面积公式即可求出S△AEB的值，此题得解．