题目内容
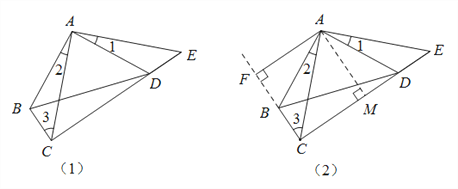
【题目】如图(1),在四边形ABCD中,已知∠ABC![]() ∠ADC
∠ADC![]() 180°,AB
180°,AB![]() AD,AB
AD,AB![]() AD,点E在CD的延长线上,∠1
AD,点E在CD的延长线上,∠1![]() ∠2.
∠2.
(1)求证:∠3![]() ∠E;
∠E;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的边BC上的高,求证:CE![]() 2AF.
2AF.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】分析:(1)根据三角形的判定定理ASA即可证得.(2)通过三角形全等求得AC=AE,∠BCA=∠E,进而根据等边对等角求得∠ACD=∠E,从而求得∠BCA=∠E=∠ACD即可证得.(3)过点A作AM⊥CE,垂足为M,根据角的平分线的性质求得AF=AM,然后证得△CAE和△ACM是等腰直角三角形,进而证得EC=2AF.
本题解析:
(1)∵![]() ,
,![]()
∴![]()
在△ABC在△ADE中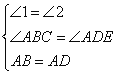
∴△ABC≌△ADE
∴![]()
(2)由(1)△ABC≌△ADE 可得
AC=AE ∴![]()
![]() 又
又
∴![]()
∴AC平分∠BCD
(3)过点A作![]() 交CE于点M
交CE于点M

∵AC平分![]() 且
且![]() ∴AF=AM ,
∴AF=AM ,
又∵![]()
∴![]() 即
即![]()
又AC=AE ∴![]()
∴△ACM和△ACE都是等腰直角三角形
∴AM=MC=ME=AF, ∴CE=2CM=2AF

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目