题目内容
 (2013•平阳县二模)如图,抛物线y=ax2+bx+
(2013•平阳县二模)如图,抛物线y=ax2+bx+| 5 |
| 2 |
| 5 |
| 2 |
(1)求抛物线的解析式;
(2)①当D为抛物线顶点时,线段DC的长度是多少?
②设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出S的最大值.
分析:(1)利用待定系数法求二次函数解析式即可得出答案;
(2)①利用配方法求出D点坐标,进而得出AB解析式,得出C点坐标,进而求出CD即可;
②由题意可得:D(m,-
m2+2m+
),C(m,
m+
),进而利用△ADB的面积为△ADC的面积+△CDB的面积,求出即可.
(2)①利用配方法求出D点坐标,进而得出AB解析式,得出C点坐标,进而求出CD即可;
②由题意可得:D(m,-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)由题意得
解:(1)由题意得
解得:
故抛物线解析式为:y=-
x2+2x+
;
(2)①∵y=-
x2+2x+
=-
(x-2)2+
,
∴顶点D(2,
)
设直线AB为:y=kx+b,
则有
解得
∴直线解析式为:y=
x+
,
当x=2时,y=
×2+
=
,
∴C(2,
)
∴CD=
-
=3,
②由题意可得:D(m,-
m2+2m+
),C(m,
m+
),
CD=(-
m2+2m+
)-(
m+
)
=-
m2+
m+2.
∴S=
(m+1)•CD+
(4-m)•CD
=
×5×CD
=
×5×(-
m2+
m+2)
=-
m2+
m+5
=-
(m-
)2+
.
∵-
<0,
∴当m=
时,S最大值为
.
 解:(1)由题意得
解:(1)由题意得
|
解得:
|
故抛物线解析式为:y=-
| 1 |
| 2 |
| 5 |
| 2 |
(2)①∵y=-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴顶点D(2,
| 9 |
| 2 |
设直线AB为:y=kx+b,
则有
|
解得
|
∴直线解析式为:y=
| 1 |
| 2 |
| 1 |
| 2 |
当x=2时,y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴C(2,
| 3 |
| 2 |
∴CD=
| 9 |
| 2 |
| 3 |
| 2 |
②由题意可得:D(m,-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
CD=(-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 3 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 5 |
| 4 |
| 15 |
| 4 |
=-
| 5 |
| 4 |
| 3 |
| 2 |
| 125 |
| 16 |
∵-
| 5 |
| 4 |
∴当m=
| 3 |
| 2 |
| 125 |
| 16 |
点评:此题主要考查了二次函数的综合应用以及待定系数法求二次函数解析式和三角形面积求法等知识,利用AB解析式得出C点坐标是解题关键.

练习册系列答案
相关题目
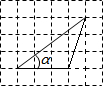 (2013•平阳县二模)三角形在方格纸中的位置如图所示,则cosα的值是( )
(2013•平阳县二模)三角形在方格纸中的位置如图所示,则cosα的值是( )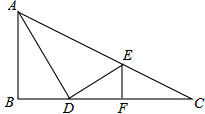 (2013•平阳县二模)如图,Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AD交AC于点E,EF⊥BC于点F,若AB=4,BD=2,则CE的长为( )
(2013•平阳县二模)如图,Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AD交AC于点E,EF⊥BC于点F,若AB=4,BD=2,则CE的长为( )