题目内容
边长为2cm的等边三角形的高为
- A.
- B.
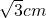
- C.
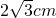
- D.1cm
B
分析：根据题意画出等边三角形ABC，过A作BC边上的高AD，交BC于D点，由AB=AC=BC，且AD垂直于BC，根据三线合一得到D为BC中点，由等边三角形的边长求出BD的长，在直角三角形ABD中，由AB及BD的长，利用勾股定理即可求出高AD的长．
解答：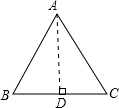
解：根据题意画出等边△ABC，过A作AD⊥BC，如图所示：
∵△ABC为等边三角形，
∴AB=AC=BC=2cm，又AD⊥BC，
∴D为BC的中点，
∴BD=CD=
BC=1cm，
在Rt△ABD中，由AB=2cm，BD=1cm，
根据勾股定理得：AD=
=
cm，
则等边三角形一边上的高为cm．
故选：B．
点评：此题考查了等边三角形的性质，等腰三角形的性质，以及勾股定理，根据题意画出相应的图形，熟练运用性质及定理是解本题的关键．
分析：根据题意画出等边三角形ABC，过A作BC边上的高AD，交BC于D点，由AB=AC=BC，且AD垂直于BC，根据三线合一得到D为BC中点，由等边三角形的边长求出BD的长，在直角三角形ABD中，由AB及BD的长，利用勾股定理即可求出高AD的长．
解答：
解：根据题意画出等边△ABC，过A作AD⊥BC，如图所示：∵△ABC为等边三角形，
∴AB=AC=BC=2cm，又AD⊥BC，
∴D为BC的中点，
∴BD=CD=
BC=1cm，在Rt△ABD中，由AB=2cm，BD=1cm，
根据勾股定理得：AD=
=cm，则等边三角形一边上的高为
cm．故选：B．
点评：此题考查了等边三角形的性质，等腰三角形的性质，以及勾股定理，根据题意画出相应的图形，熟练运用性质及定理是解本题的关键．
练习册系列答案
相关题目
16、如图，把边长为2cm的正方形剪成四个全等的直角三角形，请用这四个直角三角形拼成符合下列要求的图形．（全部用上，互不重合且不留空隙），并把你的拼法依照图示按实际大小画在方格内（方格为1cm×1cm）
如图，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动．设运动时间为t（s），解答下列问题：
