题目内容
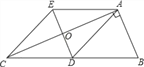
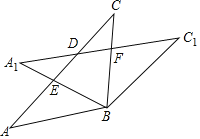
【题目】如图,在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,下列结论不一定正确的是( )
,下列结论不一定正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】C
【解析】
由旋转的性质和等腰三角形的性质可得∠ABA1=∠CBC1=α,AB=A1B=BC=BC1,∠A=∠C=∠A1=∠C1,可证△ABE≌△C1BF,△A1BF≌△CBE,可得BE=BF,A1F=CE,由三角形内角和定理可得∠CDF=∠CBC1=α.
解:∵AB=BC,∴∠A=∠C,
∵将△ABC绕点B顺时针旋转a°,得到△A1BC1,
∴∠ABA1=∠CBC1=α,AB=A1B=BC=BC1,∠A=∠C=∠A1=∠C1,
∴△ABE≌△C1BF(ASA)
∴BE=BF,故选项B不符合题意;
∵∠C=∠C1,∠DFC=∠BFC1,
∴∠CDF=∠CBC1=α,故选项A不符合题意;
∵A1B=BC,∠C=∠A1,∠A1BC=∠A1BC,
∴△A1BF≌△CBE(ASA)
∴A1F=CE,故选项D不符合题意;
由∠C不一定等于∠CDF,
∴DF不一定等于FC,
故C选项符合题意;
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目