题目内容
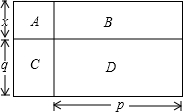如图，大长方形是由1个小正方形（A）和3个小长方形（B、C、D）拼成的，请根据图中数据解决下列问题：（1）分别写出图中四部分的面积为：
SA=
x2
x2
，SB=px
px
，SC=qx
qx
，SD=pq
pq
；（2）拼成的大长方形的长为
p+x
p+x
，宽为q+x
q+x
，面积为（p+x）（q+x）
（p+x）（q+x）
；（3）由（1）、（2）可得一个因式分解的公式为
x2+px+qx+pq=（p+x）（q+x）
x2+px+qx+pq=（p+x）（q+x）
．（4）利用（3）中的公式分解因式：x2-x-12．
分析：（1）小正方形A边长为x，表示出面积；矩形B长为p，宽为x，矩形C长为q，宽为x，矩形D长为p，宽为x，表示出各自的面积即可；
（2）大长方形的长为p+x，宽为q+x，表示出面积即可；
（3）根据A，B，C，D面积之和等于大长方形的面积列出关系式即可；
（4）利用此方法解所求式子分解因式即可．
（2）大长方形的长为p+x，宽为q+x，表示出面积即可；
（3）根据A，B，C，D面积之和等于大长方形的面积列出关系式即可；
（4）利用此方法解所求式子分解因式即可．
解答：解：（1）SA=x2，SB=px，SC=qx，SD=pq；
（2）根据题意得：大长方形的长为p+x，宽为q+x，面积为（p+x）（q+x）；
（3）根据题意得：x2+px+qx+pq=（p+x）（q+x）；
（4）根据题意得：x2-x-12=（x-4）（x+3）．
故答案为：（1）x2，px，qx，pq；（2）p+x，q+x，（p+x）（q+x）；（3）x2+px+qx+pq=（p+x）（q+x）．
（2）根据题意得：大长方形的长为p+x，宽为q+x，面积为（p+x）（q+x）；
（3）根据题意得：x2+px+qx+pq=（p+x）（q+x）；
（4）根据题意得：x2-x-12=（x-4）（x+3）．
故答案为：（1）x2，px，qx，pq；（2）p+x，q+x，（p+x）（q+x）；（3）x2+px+qx+pq=（p+x）（q+x）．
点评：此题考查了因式分解的应用，弄清题意是解本题的关键．
练习册系列答案
相关题目
（2012•六合区一模）观察猜想
=
= ( )( )． 
=
分解因式．
=
=
．
； 
．
=
=
( )( )． 
=
分解因式．
=
=
．
； 
．