Question

【题目】某公司生产一种新型生物医药产品，生产成本为2万元/ 吨，每月生产能力为12吨，且生产出的产品都能销售出去.这种产品部分内销，另一部分外销（出口），内销与外销的单价 （单位：万元/吨）与销量的关系分别如图1，图2.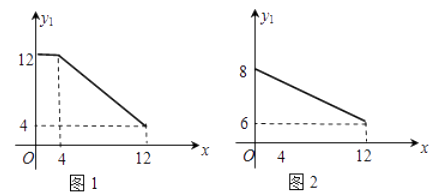

（1）如果该公司内销数量为x（单位：吨），内、外销单价分别为y 1 , y 2 ,求, 关于x的函数解析式；
（2）如果该公司内销数量为x（单位：吨），求内销获得的毛利润 关于x的函数解析式；
（3）请设计一种销售方案，使该公司本月能获得最大毛利润，并求出毛利润的最大值.（毛利润=销售收入－生产成本）.

Answer 1

【答案】
（1）解：由图1可得：当0≤x≤4时， y1=12，
当4<x≤12时，依题可设y1=kx+b，
由图1可知y1过（4，12），（12，4）两点，
∴，
∴，
∴ y1=x+16 ，
∴ y1=，
依题可设y2=cx+d，
由图2可知y2过（0，8），（12，6）两点，
∴，
∴，
∴y2=x+8（0x12），
（2）解：依题可得：
当 0≤x≤4 时， S1=(122)x=10x ；
当 4<x≤12 时， S1=(x+162)x=x2+14x；
∴S1=，
（3）解：设内销产品为x吨，则外销产品为（12-x）吨，外销毛利润为S2万元，总利润为W万元，
∵ S2=（12-x）【-（12-x）+8-2】，
当 0≤x≤4 时，
∴W=S1+S2=10x-x2-2x+48
=x2+8x+48，
=-x2-2x+48，
=-（x-24）2+144，
∵a=-，x24,
∴W随x的增大而增大，
∴当x=4时，W取得最大值，且Wmax=.
当 4x≤12 时，
W=S1+S2=x2+14x-x2-2x+48，
=x2+12x+48，
=-（x-）2+，
∵a=-，
∴当x=时，W取得最大值，且Wmax=.
∵ ，
综上所述：当x=时，W取得最大值，且Wmax=.
∴当安排内销吨，外销吨时，该公司本月可以获得最大毛利润万元.

【解析】（1）由图1可知分0≤x≤4和4<x≤12 两种情况，利用待定系数法即可求得y1解析式；由图2利用待定系数法即可求得y2解析式.
（2）根据毛利润=销售收入－生产成本，由（1）求出的解析式分0≤x≤4和4<x≤12 两种情况，即可求得.
（3）设内销产品为x吨，则外销产品为（12-x）吨，外销毛利润为S2万元，总利润为W万元，根据（2）中的关系式列出S2的解析式，再分0≤x≤4和4<x≤12 两种情况，由W=S1+S2求得二次函数解析式，依据二次函数的性质求出函数最值即可.