��Ŀ����
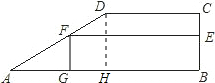
��ͼ����ֱ������ABCD�У�AB��CD����ABC=90�㣬AB=2a��CD=a��BC=2���ı���BEFG�Ǿ��Σ���E ��F�ֱ�����BC��AD�ϣ���G��AB�ϣ���FG=x������BEFG�����Ϊy��
��F�ֱ�����BC��AD�ϣ���G��AB�ϣ���FG=x������BEFG�����Ϊy����1����y����x�ĺ�����ϵʽ��
��2��������BEFG�������������ABCD�������һ��ʱ����x��ֵ��
��3������DAB=30��ʱ������BEFG�Ƿ��ܳ�Ϊ�����Σ����ܣ�����߳��������ܣ���˵�����ɣ�
��������1������D��DH��AB��H�����ڡ�AGF�ס�AHD���õ�AG��ֵ����BG=AB-AG��������y=S����=FG•BG���õ�y����x�ĺ�����ϵʽ��
��2��������ε�������ɾ���BEFG�������������ABCD�������һ�뽨�����̣����x��ֵ��
��3�������еĸ���ɵõ�CD=2
���Ӷ��õ�EF��2��FG���ʾ���BEFG���ܳ�Ϊ�����Σ�
��2��������ε�������ɾ���BEFG�������������ABCD�������һ�뽨�����̣����x��ֵ��
��3�������еĸ���ɵõ�CD=2
| 3 |
��� �⣺��1������D��DH��AB��H��
�⣺��1������D��DH��AB��H��
���ھ���BEFG�У�FG��AB������FG��DH��
���AGF�ס�AHD��
��
=
��
��
=
����AG=
��
��BG=AB-AG=2a-
=
��
���y=FG•BG=x��
=-
ax2+2ax��
��y=FG•BG=x��
=-
ax2+2ax��
������ĺ�����ϵʽΪy=-
ax2+2ax ��0��x��2����
��2�������⣬��-
ax2+2ax=
��
��a+2a����2��
��Ϊa��0�������Ϸ��̵ã�x1=1��x2=3��
��Ϊ0��x��2������x=3��ȥ��ȡx=1��
�ʵ�����BEFG�������������ABCD�������һ��ʱ��x��ֵΪ1��
��3������BEFG���ܳ�Ϊ�����Σ�
��Rt��AHD�У��ߡ�DAH=30�㣬��tan30��=
=
����a=2
EF��CD=a=2
����EF��2��
�֡�0��x��2����0��FG��2����EF��FG��
��˾���BEFG���ܳ�Ϊ�����Σ�
 �⣺��1������D��DH��AB��H��
�⣺��1������D��DH��AB��H�����ھ���BEFG�У�FG��AB������FG��DH��
���AGF�ס�AHD��
��
| AG |
| AH |
| FG |
| DH |
��
| AG |
| 2a-a |
| x |
| 2 |
| ax |
| 2 |
��BG=AB-AG=2a-
| ax |
| 2 |
| 4a-ax |
| 2 |
���y=FG•BG=x��
| 4a-ax |
| 2 |
| 1 |
| 2 |
��y=FG•BG=x��
| 4a-ax |
| 2 |
| 1 |
| 2 |
������ĺ�����ϵʽΪy=-
| 1 |
| 2 |
��2�������⣬��-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��Ϊa��0�������Ϸ��̵ã�x1=1��x2=3��
��Ϊ0��x��2������x=3��ȥ��ȡx=1��
�ʵ�����BEFG�������������ABCD�������һ��ʱ��x��ֵΪ1��
��3������BEFG���ܳ�Ϊ�����Σ�
��Rt��AHD�У��ߡ�DAH=30�㣬��tan30��=
| DH |
| AH |
| 2 |
| a |
| 3 |
EF��CD=a=2
| 3 |
�֡�0��x��2����0��FG��2����EF��FG��
��˾���BEFG���ܳ�Ϊ�����Σ�
�������������������κ;��ε����ʣ����������ε��ж������ʣ����еĸ�����⣬��Ӧ����һԪ���η��̵Ľⷨ��

��ϰ��ϵ�д�
�����Ŀ
 20����ͼ����ֱ������ABCD�У�AD��BC��CD��BC��EΪBC���ϵĵ㣮��ֱ������ABCD�ضԽ���BD�۵���ʹ��ABD���EBD�غϣ���ͼ����Ӱ��ʾ��������A=130�㣬AB=4cm��������ABCD�ĸ�CD��
20����ͼ����ֱ������ABCD�У�AD��BC��CD��BC��EΪBC���ϵĵ㣮��ֱ������ABCD�ضԽ���BD�۵���ʹ��ABD���EBD�غϣ���ͼ����Ӱ��ʾ��������A=130�㣬AB=4cm��������ABCD�ĸ�CD�� ��ͼ����ֱ������ABCD�У�AB��DC����D=90�㣬AC��BC��AB=10cm��BC=6cm��F����2cm/����ٶ����߶�AB����A��B�����˶���E��ͬʱ��1cm/����ٶ����߶�BC����B��C�����˶������˶�ʱ��Ϊt�루0��t��5����
��ͼ����ֱ������ABCD�У�AB��DC����D=90�㣬AC��BC��AB=10cm��BC=6cm��F����2cm/����ٶ����߶�AB����A��B�����˶���E��ͬʱ��1cm/����ٶ����߶�BC����B��C�����˶������˶�ʱ��Ϊt�루0��t��5���� ��1998•��������ͼ����ֱ������ABCD�У�AD��BC��DC��BC����BC=3AD�������εĸ�AEΪֱ���ġ�O��AB�ڵ�F����CD�ڵ�G��H������F����O�����߽�BC�ڵ�N��
��1998•��������ͼ����ֱ������ABCD�У�AD��BC��DC��BC����BC=3AD�������εĸ�AEΪֱ���ġ�O��AB�ڵ�F����CD�ڵ�G��H������F����O�����߽�BC�ڵ�N�� BC�ϵĶ��㣬��G��AB�ϣ����ı���AEFG�Ǿ��Σ���FG=x������AEFG�����Ϊy��
BC�ϵĶ��㣬��G��AB�ϣ����ı���AEFG�Ǿ��Σ���FG=x������AEFG�����Ϊy��