Question

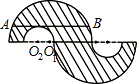
在某校校园文化建设活动中，小彬同学为班级设计了一个班徽，这个班徽图案由一对大小相同的较大半圆挖去一对大小相同的较小半圆而得．如图，若它们的直径在同一直线上，较大半圆O₁的弦AB∥O₁O₂，且与较小半圆O₂相切，AB=4，则班徽图案的面积为

1. A.
   25π
2. B.
   16π
3. C.
   8π
4. D.
   4π

Answer 1

D
分析：由题意可知班徽图案的面积=大雨的面积-小圆的面积即圆环面积．
解答：平移小圆使O₁和O₂重合，
设与较小半圆O₂相切的切点为C，连接0₁C，O₁A，

∴O₁C⊥AB，
∴AC=BC=AB=2，
∵S_阴影=S_大-S_小=π（AO₁²-O₁C₁²）=πAC²=4π．
故选D．
点评：本题考查了圆的面积公式和垂径定理、切线的性质定理的运用，解题的关键是把阴影部分面积转化为圆环的面积．