题目内容
在△ABC中,(tanC-1)2+| -2cosB|=0,则∠A=________.
-2cosB|=0,则∠A=________.
105°
分析:先利用两个非负数的和等于0,则每一个非负数等于0,可求B、C,再利用三角形内角和定理可求A.
解答:∵(tanC-1)2+| -2cosB|=0,
-2cosB|=0,
∴tanC-1=0, -2cosB=0,
-2cosB=0,
即tanC=1,cosB= ,
,
又∵B、C在同一个三角形中,
∴B=30°,C=45°,
∴A=180°-30°-45°=105°.
故答案是105°.
点评:本题考查实数的综合运算能力、非负数的性质、绝对值,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值.
分析:先利用两个非负数的和等于0,则每一个非负数等于0,可求B、C,再利用三角形内角和定理可求A.
解答:∵(tanC-1)2+|
 -2cosB|=0,
-2cosB|=0,∴tanC-1=0,
 -2cosB=0,
-2cosB=0,即tanC=1,cosB=
 ,
,又∵B、C在同一个三角形中,
∴B=30°,C=45°,
∴A=180°-30°-45°=105°.
故答案是105°.
点评:本题考查实数的综合运算能力、非负数的性质、绝对值,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
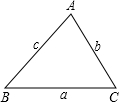 如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答:
如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答: