题目内容
【题目】问题提出
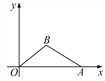
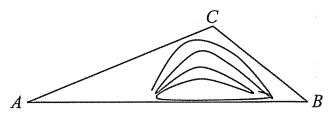
(1)如图1,已知三角形![]() ,请在
,请在![]() 边上确定一点
边上确定一点![]() ,使得
,使得![]() 的值最小.
的值最小.
问题探究
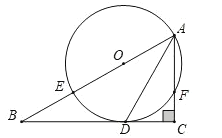
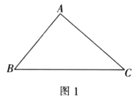
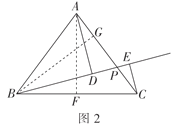
(2)如图2,在等腰![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一动点,分别过点
边上一动点,分别过点![]() ,点
,点![]() 作线段
作线段![]() 所在直线的垂线,垂足为点
所在直线的垂线,垂足为点![]() ,若
,若![]() ,求线段
,求线段![]() 的取值范围,并求
的取值范围,并求![]() 的最大值.
的最大值.
问题解决
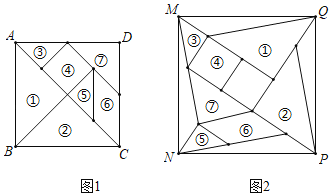
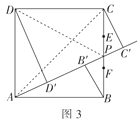
(3)如图3,正方形![]() 是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点
是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点![]() 处和
处和![]() 边的两个三等分点
边的两个三等分点![]() 之间的某点
之间的某点![]() 建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为
建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为![]() 、
、![]() 、
、![]() .若你是此次项目设计的负责人,要使三条运输轨道的距离之和
.若你是此次项目设计的负责人,要使三条运输轨道的距离之和![]() 最小,你能不能按照要求进行规划,请通过计算说明.
最小,你能不能按照要求进行规划,请通过计算说明.

【答案】(1)答案见解析;(2)![]() 的取值范围是
的取值范围是![]() ,当
,当![]() 取最小值
取最小值![]() 时,
时,![]() 取得最大值,最大值是5;(3)可以按照要求进行规划(点P选在点E处),三条输送轨道之和最小为
取得最大值,最大值是5;(3)可以按照要求进行规划(点P选在点E处),三条输送轨道之和最小为![]() 千米.
千米.
【解析】
(1)根据垂线段最短即可得;
(2)如图2(见解析),先根据等腰三角形的性质、勾股定理求出![]() ,再根据等面积法可求出
,再根据等面积法可求出![]() ,由此即可得线段
,由此即可得线段![]() 的取值范围;然后根据
的取值范围;然后根据![]() 可得当
可得当![]() 取最小值时,
取最小值时,![]() 取得最大值,将BP的最小值代入求解即可得;
取得最大值,将BP的最小值代入求解即可得;
(3)如图3(见解析),连接![]() ,先参照(2)的方法求出AP的取值范围,再根据
,先参照(2)的方法求出AP的取值范围,再根据![]() 得出
得出![]() ,由此即可得出答案.
,由此即可得出答案.
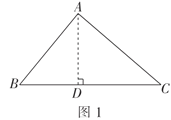
(1)如图1,过点![]() 作
作![]() ,垂足为点
,垂足为点![]()
由垂线段最短可知,此时![]() 的值最小;
的值最小;
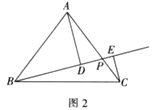
(2)如图2,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]()
![]()
![]() 是等腰三角形
是等腰三角形
![]()
![]()
由等面积法得:![]() ,即
,即![]()
解得![]()
![]() 点
点![]() 在
在![]() 边上,
边上,![]()
![]() ,即
,即![]()
则![]() 的取值范围是
的取值范围是![]()
![]()
![]() 当
当![]() 取最小值
取最小值![]() 时,
时,![]() 取得最大值
取得最大值
将![]() 代入得:
代入得:![]()
解得![]()
则![]() 的最大值是5;
的最大值是5;
(3)如图3,连接![]()
![]() 正方形
正方形![]() 边长为3,
边长为3,![]() 为
为![]() 边的三等分点
边的三等分点
![]()
参考(2)可知,![]()
即![]()
![]() ,即
,即![]()
又![]()
![]()
即![]()
![]() 当
当![]() 取最大值
取最大值![]() 时,
时,![]() 取得最小值
取得最小值
将![]() 代入得:
代入得:![]()
解得![]()
则![]() 的最小值为
的最小值为![]()
综上,可以按照要求进行规划(点P选在点E处),三条输送轨道之和最小为![]() 千米.
千米.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】已知函数![]() ,小李同学对该函数的图象与性质进行了探究,下面是小李同学探究的过程,补充完整:
,小李同学对该函数的图象与性质进行了探究,下面是小李同学探究的过程,补充完整:
(1)直接写出自变量x的取值范围:__________;
(2)下表是y与x的几组对应值:
x | … | -4 | -1 | 0 |
| 1 |
|
| 3 |
| 4 | 5 | n | … |
y | … |
| m |
| 0 | -1 | -4 | 8 | 5 | 4 |
| 3 |
| … |
则m= ,n= ;
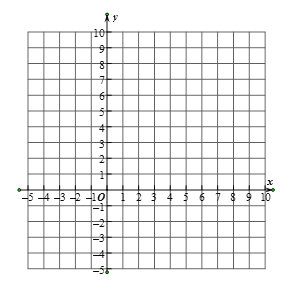
(3)如图所示,在平面直角坐标系xoy中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象;
(4)观察函数图象可知:该函数图象的对称中心的坐标是______;
(5)当![]() 时,关于x的方程
时,关于x的方程![]() 有实数解,直接写出k的取值范围_______.
有实数解,直接写出k的取值范围_______.