题目内容
在等边三角形ABC中,D为AC上一点,且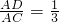 ,要在AB上取一点E,使△ADE∽△CDB,则
,要在AB上取一点E,使△ADE∽△CDB,则 等于
等于
- A.

- B.

- C.

- D.1
C
分析:首先根据题意作图,由△ABC是等边三角形,即可得∠A=∠C=60°,AC=BC,又由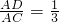 ,求得
,求得 ,然后由当
,然后由当 时,则△ADE∽△CDB,根据比例的性质,即可求得
时,则△ADE∽△CDB,根据比例的性质,即可求得 的值,继而求得
的值,继而求得 的值.
的值.
解答: 解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,
∴∠A=∠C=60°,AC=BC,
∵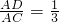 ,
,
∴ ,
,
当 时,则△ADE∽△CDB,
时,则△ADE∽△CDB,
即 ,
,
∴ =
= .
.
故选C.
点评:此题考查了相似三角形的判定与性质,等边三角形的性质以及比例变形.此题难度适中,解题的关键是注意数形结合思想的应用,注意比例变形.
分析:首先根据题意作图,由△ABC是等边三角形,即可得∠A=∠C=60°,AC=BC,又由
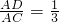 ,求得
,求得 ,然后由当
,然后由当 时,则△ADE∽△CDB,根据比例的性质,即可求得
时,则△ADE∽△CDB,根据比例的性质,即可求得 的值,继而求得
的值,继而求得 的值.
的值.解答:
 解:∵△ABC是等边三角形,
解:∵△ABC是等边三角形,∴∠A=∠C=60°,AC=BC,
∵
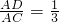 ,
,∴
 ,
,当
 时,则△ADE∽△CDB,
时,则△ADE∽△CDB,即
 ,
,∴
 =
= .
.故选C.
点评:此题考查了相似三角形的判定与性质,等边三角形的性质以及比例变形.此题难度适中,解题的关键是注意数形结合思想的应用,注意比例变形.

练习册系列答案
相关题目
 20、如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理.
20、如图所示,在等边三角形ABC中,∠B、∠C的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理. 17、如图,已知在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE.
17、如图,已知在等边三角形ABC中,D、E是AB、AC上的点,且AD=CE. 已知:如图,在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD=CE.
已知:如图,在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD=CE. 如图,在等边三角形ABC中,D为AC的中点,
如图,在等边三角形ABC中,D为AC的中点,