Question

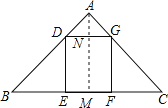
【题目】如图1，在△ABC中，AB=AC=5，BC=6，正方形DEFG的顶点D、G分别在AB、AC上，EF在BC上．

（1）求正方形DEFG的边长；

（2）如图2，在BC边上放两个小正方形DEFG、FGMN，则DE= ．

Answer 1

【答案】（1）；（2）．

【解析】

试题分析：（1）过点作AM⊥BC于点M，由AB=AC=10，BC=16，根据等腰三角形的性质与勾股定理，即可求得AM的长，又由四边形DEFG是矩形，易证得△ADG∽△ABC，设MN=DE=x，由相似三角形对应高的比等于相似比，即可得方程，则可表示出DG的长，由正方形的性质可得DE=DG，可得结果；

（2）由题意得：DN=2DE，由（1）知：，即可得到结论．

解：过点作AM⊥BC于点M，

∵AB=AC=5，BC=6，

∴BM=BC=3，

在Rt△ABM中，AM==4，

∵四边形DEFG是矩形，

∴DG∥EF，DE⊥BC，

∴AN⊥DG，四边形EDMN是矩形，

∴MN=DE，

设MN=DE=x，

∵DG∥EF，

∴△ADG∽△ABC，

∴DG：BC=AN：AM，

∴，

解得：DG=﹣x+6，

∵四边形DEFG为正方形，

∴DE=DG，即x=﹣x+6，

解得x=，

∴正方形DEFG的边长为；

（2）由题意得：DN=2DE，

由（1）知：，

∴DE=．

故答案为：．