题目内容
⊙O的半径长为10,点P到圆心的距离为8,经过点P且长为整数的弦有几条
- A.9
- B.12
- C.14
- D.16
D
分析:根据题意画出图形,CD为过P点的直径,AB为过P点与CD垂直的弦,连OA,则AP=BP,而⊙0的半径为10,OP=8,由勾股定理可得到最短的弦长AB的长,由CD为过P点的直径可得出CD是过点P最长的弦,由此可得出经过点P且长为整数的弦的长度,又根据圆的对称性即可得出结论.
解答: 解:如图,CD为过P点的直径,AB为过P点与CD垂直的弦,连OA,
解:如图,CD为过P点的直径,AB为过P点与CD垂直的弦,连OA,
∵AB⊥CD,
∴AP=BP,
∵⊙0的半径为10,OP=8,
∴过P点的最长的弦是直径CD=20,
最短的弦长AB=2AP=2 =2
=2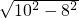 =12,
=12,
∴⊙O中,过P点的弦长L的取值范围是12≤L≤20,
∵L为整数,
∴L的值可取12,13,14,15,16,17,18,19,20,
又根据圆的对称性知:长度为13,14,15,16,17,18,19的弦各有2条,
∴通过P点且长度是整数值的弦的条数是16.
故选D.
点评:本题考查的是垂径定理及勾股定理,根据题意画出图形,作出辅助线,构造出直角三角形是解答此题的关键.
分析:根据题意画出图形,CD为过P点的直径,AB为过P点与CD垂直的弦,连OA,则AP=BP,而⊙0的半径为10,OP=8,由勾股定理可得到最短的弦长AB的长,由CD为过P点的直径可得出CD是过点P最长的弦,由此可得出经过点P且长为整数的弦的长度,又根据圆的对称性即可得出结论.
解答:
 解:如图,CD为过P点的直径,AB为过P点与CD垂直的弦,连OA,
解:如图,CD为过P点的直径,AB为过P点与CD垂直的弦,连OA,∵AB⊥CD,
∴AP=BP,
∵⊙0的半径为10,OP=8,
∴过P点的最长的弦是直径CD=20,
最短的弦长AB=2AP=2
 =2
=2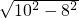 =12,
=12,∴⊙O中,过P点的弦长L的取值范围是12≤L≤20,
∵L为整数,
∴L的值可取12,13,14,15,16,17,18,19,20,
又根据圆的对称性知:长度为13,14,15,16,17,18,19的弦各有2条,
∴通过P点且长度是整数值的弦的条数是16.
故选D.
点评:本题考查的是垂径定理及勾股定理,根据题意画出图形,作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 16、如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是
16、如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是565
元(结果保留整数).已知一个扇形的弧长为10πcm,圆心角是150°,则它的半径长为( )
| A、12cm | B、10cm | C、8cm | D、6cm |