题目内容
如图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为( )
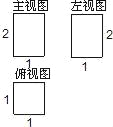
A. 2cm3 B. 4cm3 C. 6cm3 D. 8cm3
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
题目内容
如图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为( )

A. 2cm3 B. 4cm3 C. 6cm3 D. 8cm3
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案