题目内容
 如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=x m,长方形的面积为y m2,要使长方形的面积最大,其边长x应为
如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=x m,长方形的面积为y m2,要使长方形的面积最大,其边长x应为
- A.
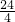 m
m - B.6m
- C.15m
- D.
 m
m
D
分析:本题考查二次函数最小(大)值的求法.思路是:长方形的面积=大三角形的面积-两个小三角形的面积.
解答:根据题意得:y=30- (5-x)
(5-x) -
- x(12-
x(12- ),
),
整理得y=- x2+12x,
x2+12x,
=- [x2-5x+(
[x2-5x+( )2-
)2- ],
],
=- (x-
(x- )2+15,
)2+15,
∵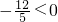
∴长方形面积有最大值,此时边长x应为 m.
m.
故选D.
点评:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数a的绝对值是较小的整数时,用配方法较好,如y=-x2-2x+5,y=3x2-6x+1等用配方法求解比较简单.
分析:本题考查二次函数最小(大)值的求法.思路是:长方形的面积=大三角形的面积-两个小三角形的面积.
解答:根据题意得:y=30-
 (5-x)
(5-x) -
- x(12-
x(12- ),
),整理得y=-
 x2+12x,
x2+12x,=-
 [x2-5x+(
[x2-5x+( )2-
)2- ],
],=-
 (x-
(x- )2+15,
)2+15,∵
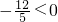
∴长方形面积有最大值,此时边长x应为
 m.
m.故选D.
点评:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数a的绝对值是较小的整数时,用配方法较好,如y=-x2-2x+5,y=3x2-6x+1等用配方法求解比较简单.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=x m,长方形的面积为y m2,要使长方形的面积最大,其边长x应为( )
如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=x m,长方形的面积为y m2,要使长方形的面积最大,其边长x应为( )A、
| ||
| B、6m | ||
| C、15m | ||
D、
|
 如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
 m
m m
m
 m
m m
m
 m
m m
m