题目内容
 甲、乙两人骑自行车分别从相距一定距离的A、B 两地相向而行.假设他们都保持匀速行驶,他们各自到A地的距离s(千米)都是骑车时间t(时)的函数,图象如图所示.根据图象解决下列问题:
甲、乙两人骑自行车分别从相距一定距离的A、B 两地相向而行.假设他们都保持匀速行驶,他们各自到A地的距离s(千米)都是骑车时间t(时)的函数,图象如图所示.根据图象解决下列问题:
(1)出发时______在A地,A、B两地相距______千米.
(2)v甲______千米/时,v乙______千米/时.
(3)分别求出甲、乙在行驶过程中s(千米)与t(时)的函数关系式.
解:(1)∵根据函数的图象可得:
出发时甲离A地的距离是0千米,乙离A地的距离是150千米,
∴出发时甲在A地,A、B两地相距150千米;
(2)设甲的函数关系式为L甲=k1t(k1≠0),乙的函数关系式为L乙=k2t+b(k2≠0),
由图象可知40=2k1,
 ,
,
解得k1=20,k2=-30,
则V甲=20(千米/小时),V乙=30(千米/小时);
(3)由(2)可知,甲、乙在行驶过程中s(千米)与t(时)的函数关系式分别是s甲=20t和s乙=-30t+150.
故答案为:甲,150;20,30.
分析:(1)根据函数的图象可直接得出,出发时甲离A地的距离和乙离A地的距离,即可得出答案;
(2)先设甲的函数关系式为L甲=k1t(k1≠0),乙的函数关系式为L乙=k2t+b(k2≠0),再把它们经过的点分别代入,求出甲、乙的解析式,再根据两直线的斜率,即可得出甲、乙的速度;
(3)由(2)可直接得出甲、乙在行驶过程中s(千米)与t(时)的函数关系式.
点评:本题考查了一次函数的应用,用到的知识点是用待定系数法求函数的解析式,关键是读懂题意,根据图象找出关键点的坐标,求得两个函数的解析式.
出发时甲离A地的距离是0千米,乙离A地的距离是150千米,
∴出发时甲在A地,A、B两地相距150千米;
(2)设甲的函数关系式为L甲=k1t(k1≠0),乙的函数关系式为L乙=k2t+b(k2≠0),
由图象可知40=2k1,
 ,
,解得k1=20,k2=-30,
则V甲=20(千米/小时),V乙=30(千米/小时);
(3)由(2)可知,甲、乙在行驶过程中s(千米)与t(时)的函数关系式分别是s甲=20t和s乙=-30t+150.
故答案为:甲,150;20,30.
分析:(1)根据函数的图象可直接得出,出发时甲离A地的距离和乙离A地的距离,即可得出答案;
(2)先设甲的函数关系式为L甲=k1t(k1≠0),乙的函数关系式为L乙=k2t+b(k2≠0),再把它们经过的点分别代入,求出甲、乙的解析式,再根据两直线的斜率,即可得出甲、乙的速度;
(3)由(2)可直接得出甲、乙在行驶过程中s(千米)与t(时)的函数关系式.
点评:本题考查了一次函数的应用,用到的知识点是用待定系数法求函数的解析式,关键是读懂题意,根据图象找出关键点的坐标,求得两个函数的解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 6、如图是公园的路线图,⊙O1,⊙O2,⊙O两两相切,点A,B,O分别是切点,甲乙二人骑自行车,同时从点A出发,以相同的速度,甲按照“圆”形线行驶,乙行驶“8字型”线路行驶.若不考虑其他因素,结果先回到出发点的人是( )
6、如图是公园的路线图,⊙O1,⊙O2,⊙O两两相切,点A,B,O分别是切点,甲乙二人骑自行车,同时从点A出发,以相同的速度,甲按照“圆”形线行驶,乙行驶“8字型”线路行驶.若不考虑其他因素,结果先回到出发点的人是( )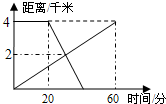 已知A、B两地相距4千米.上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲、乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为
已知A、B两地相距4千米.上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲、乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为 已知A、B两地相距6千米,上午8:00,甲从A地出发步行到B地;8:20后,乙从B地出发骑自行车到A地,甲、乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示.
已知A、B两地相距6千米,上午8:00,甲从A地出发步行到B地;8:20后,乙从B地出发骑自行车到A地,甲、乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示.