Question

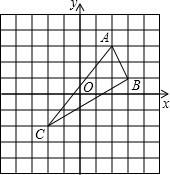
如图，已知△ABC 三个顶点的坐标分别为（1，2），（-2，3），（-1，0）。把它们的横坐标和纵坐标分别变成原来的2倍，得到点A、B、C，下列说法正确的是

1. A.
   △A/B/C/和△ABC是位似图形，位似中心是（1，0）。
2. B.
   △A/B/C/和△ABC是位似图形，位似中心是（0，0）。
3. C.
   △A/B/C/和△ABC是相似图形，但不是位似图形。
4. D.
   △A/B/C/和△ABC不是相似图形。

Answer 1

B
考点：位似变换；待定系数法求一次函数解析式．
分析：根据位似图形的性质可知，△ABC三个顶点的坐标分别为（1，2），（-2，3），（-1，0），把它们的横坐标和纵坐标都扩大到原来的2倍，可求得直线AA′，BB′，CC′得解析式分别为y=2x，y=-x，y=0，所以可知△A′B′C′与△ABC是位似图形，位似中心是点（0，0）．解答：解：∵△ABC三个顶点的坐标分别为（1，2），（-2，3），（-1，0），把它们的横坐标和纵坐标都扩大到原来的2倍
∴点A′，B′，C′的坐标分别为（2，4），（-4，6），（-2，0）
∴直线AA′，BB′，CC′得解析式分别为y=2x，y=- x，y=0
∴对应点的连线交于原点
∴△A′B′C′与△ABC是位似图形，位似中心是点（0，0）
故选B．
点评：本题考查了位似的相关知识，位似是相似的特殊形式，位似图形的对应点的连线交于一点．