Question

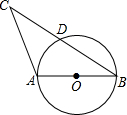
如图，⊙O的直径DF与弦AB交于点E，C为⊙O外一点，CB⊥AB于点B，G是直线CD上一点，∠ADG=∠ABD，AD∥CE．
（1）求证：AD•CE=DE•DF．
（2）若∠DAE=30°，BC=2，AD=

5

2

，AE：BE=2：3，求

BD

的长．

Answer 1

（1）证明：连接AF，OB，
∵DF是⊙O的直径，
∴∠DAF=90°，
∵∠ADG=∠ABD，
而∠F=∠ABD．
∴∠ADG=∠F，
∵∠F+∠1=90°，
∴∠ADG+∠1=90°，
∴CG是⊙O的切线．
∴∠CDE=90°，
∵AD∥CE，
∴∠1=∠2，
∴△ADF∽△DEC，
∴

AD

DF

=

DE

CE

，
即AD•CE=DE•DF．

（2）∵AD∥CE，∠DAE=30°，
∴∠CEB=∠DAE=30°，
在Rt△EBC中，∵BC=2，
∴CE=4，BE=2

3

，
∵AE：BE=2：3，
∴AE=

4 3

3

，
设DE=x，DF=y
∵AD•CE=DE•DF，AD=

5

2

，
∴xy=10，
∵由AE•BE=DE•EF，得

4 3

3

×2

3

=x（y-x），
解得x²=2，
x=

2

，
∴y=5

2

，
连接OB，于是∠DOB=60°，
∴

BD

的长为

60π× 5 2 2

180

=

5 2 π

6

，
答：

BD

的长为

5 2 π

6

．