��Ŀ����
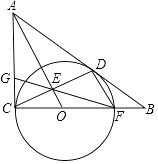
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ύ�ڵ�B����y�ύ�ڵ�A���뷴��������y= ![]() ��ͼ���ڵڶ�������C��CE��x�ᣬ����Ϊ��E��tan��ABO=
��ͼ���ڵڶ�������C��CE��x�ᣬ����Ϊ��E��tan��ABO= ![]() ��OB=4��OE=2��
��OB=4��OE=2��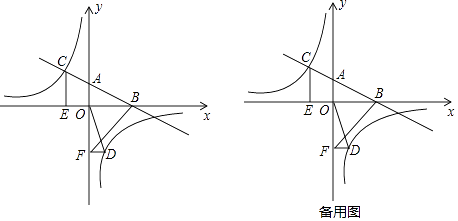
��1�����������Ľ���ʽ��
��2������D�Ƿ���������ͼ���ڵ��������ڵĵ㣬����D��DF��y�ᣬ����Ϊ��F������OD��BF�����S��BAF=4S��DFO �� ���D�����꣮
��3��������D�ڷ���������ͼ��ĵ����������˶������߶�DC���߶�DB֮��ﵽ���ʱ�����D�����꣮
���𰸡�
��1��
�⣺��tan��ABO= ![]() ��
��
�� ![]() =
= ![]() ����OB=4��
����OB=4��
��OA=2��
��CE��x�ᣬ��CE��AO��
���AOB�ס�CEB��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����CE=3��
�����CE=3��
��C����2��3����
��m=��2��3=��6��
�෴������������ʽΪy=�� ![]()
��2��
�⣺��D��x���� ![]() ����
����
��D�ڵ������ޣ�
��DF=x��OF= ![]() ��
��
��S��DFO= ![]() DFOF=
DFOF= ![]() x��
x�� ![]() =3��
=3��
�ɣ�1����֪OA=2��
��AF=x+ ![]() ��
��
��S��BAF= ![]() AFOB=
AFOB= ![]() ��x+
��x+ ![]() ����4=2��x+
����4=2��x+ ![]() ����
����
��S��BAF=4S��DFO��
��2��x+ ![]() ��=4��3�����x=3+
��=4��3�����x=3+ ![]() ��x=3��
��x=3�� ![]() ��
��
��x=3+ ![]() ʱ����
ʱ���� ![]() ��ֵΪ3��
��ֵΪ3�� ![]() ��
��
��x=3�� ![]() ʱ����
ʱ���� ![]() ��ֵΪ3+
��ֵΪ3+ ![]() ��
��
��D�ڵ������ޣ�
��x=3�� ![]() �������⣬��ȥ��
�������⣬��ȥ��
��D��3+ ![]() ��3��
��3�� ![]() ��
��
��3��
�⣺��D�ڵ������ޣ�
���ڡ�BCD�У������������߹�ϵ��֪CD��CB��BC������B��C��D���㹲��ʱ��������
��ֱ��AB����ʽΪy=kx+b��
������ɵ� ![]() �����
����� 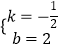 ��
��
��ֱ��AB����ʽΪy=�� ![]() x+2��
x+2��
����ֱ��AB�ͷ�������������ʽ�ɵ� 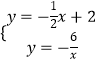 �����
����� ![]() ��
�� ![]() ����ȥ����
����ȥ����
��D��6����1����
�����߶�DC���߶�DB֮��ﵽ���ʱ���D������Ϊ��6����1��
����������1�������������OA���ɡ�AOB�ס�CEB�����CE��������C�����꣬���뷴������������ʽ�����m��ֵ������÷�������������ʽ����2�����D�����꣬�Ӷ��ɷֱ��ʾ����BAF�͡�DFO����������������г����̣��Ӷ������D�����ꣻ��3���ڡ�BCD�У������������߹�ϵ��֪CD��CB��BC����B��C��D���㹲��ʱ������������ֱ��BC�뷴������������ʽ�����D�����꣮
�����㾫����������Ĺؼ��������ⷴ�������������ʵ����֪ʶ����������:��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵ�һ���������ޣ���ÿ��������yֵ��xֵ���������С�� ��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵڶ����������ޣ���ÿ��������yֵ��xֵ������������Լ������������߹�ϵ�����⣬�˽�����������֮�ʹ��ڵ����ߣ�����������֮��С�ڵ����ߣ������϶����������߶Σ�������������ε����ߣ�

 �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д� ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д�