题目内容
(2012•无锡一模)(1)阅读理解
先观察和计算,并用“>”、“<”、“≥”、“≤”、“=”填空:4+9
,
4+4
,2+3
.请猜想:当a>0,b>0,则a+b
.
如∵(
-
)2>0,展开(
)2+(
)2-2
>0,∴6+5>2
.
请你给出猜想的一个相仿的说明过程.
(2)知识应用
①如图⊙O中,⊙O的半径为5,点P为⊙O内一个定点,OP=2,过点P作两条互相垂直的弦,即AC⊥BD,作ON⊥BD,OM⊥AC,垂足为P、N,求OM2+ON2的值.
②在上述基础上,连接AB、BC、CD、DA,利用①中的结论,探求四边形ABCD面积的最大值.

先观察和计算,并用“>”、“<”、“≥”、“≤”、“=”填空:4+9
>
>
2| 4×9 |
4+4
=
=
2| 4×4 |
>
>
2| 2×3 |
≥
≥
2| ab |
如∵(
| 6 |
| 5 |
| 6 |
| 5 |
| 6×5 |
| 6×5 |
请你给出猜想的一个相仿的说明过程.
(2)知识应用
①如图⊙O中,⊙O的半径为5,点P为⊙O内一个定点,OP=2,过点P作两条互相垂直的弦,即AC⊥BD,作ON⊥BD,OM⊥AC,垂足为P、N,求OM2+ON2的值.
②在上述基础上,连接AB、BC、CD、DA,利用①中的结论,探求四边形ABCD面积的最大值.


分析:(1)求出式子的结果,再比较即可;根据完全平方公式大于等于0,展开即可得出答案;
(2)①根据矩形的判定得出矩形MPNO,根据矩形性质得出MN=OP=2,根据勾股定理求出即可;②根据垂径定理求出AC=2CM,BD=2BN,根据勾股定理求出BN2+CM2的值,最后根据以上结论即可求出S≤46,求出答案即可.
(2)①根据矩形的判定得出矩形MPNO,根据矩形性质得出MN=OP=2,根据勾股定理求出即可;②根据垂径定理求出AC=2CM,BD=2BN,根据勾股定理求出BN2+CM2的值,最后根据以上结论即可求出S≤46,求出答案即可.
解答:(1)解:4+9>2
,4+4=2
,2+3>2
,
猜想a+b≥2
,
理由是:∵(
-
)2≥0,
∴化简得a+b≥2
,
故答案为:>,=,>,≥.
(2)①解:连接OP,MN,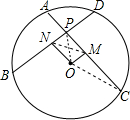
∵OM⊥BD,ON⊥AC,AC⊥BD,
∴∠PNO=∠NPM=∠PMO=90°,
∴四边形MPNO是矩形,
∴OP=MN,
∴OM2+ON2=MN2=OP2=4.
②解:连接OC,
∵由勾股定理得:MC2=OC2-OM2=25-OM2,同理BN2=25-ON2,
∴BN2+CM2=50-(OM2+ON2)=50-4=46,
∵S=
AC×BD=
×2BN×2CM=2BN×CM≤BN2+CM2,
∴S≤46,
即四边形ABCD的面积的最大值是46.
| 4 |
| 4+4 |
| 2×3 |
猜想a+b≥2
| ab |
理由是:∵(
| a |
| b |
∴化简得a+b≥2
| ab |
故答案为:>,=,>,≥.
(2)①解:连接OP,MN,

∵OM⊥BD,ON⊥AC,AC⊥BD,
∴∠PNO=∠NPM=∠PMO=90°,
∴四边形MPNO是矩形,
∴OP=MN,
∴OM2+ON2=MN2=OP2=4.
②解:连接OC,
∵由勾股定理得:MC2=OC2-OM2=25-OM2,同理BN2=25-ON2,
∴BN2+CM2=50-(OM2+ON2)=50-4=46,
∵S=
| 1 |
| 2 |
| 1 |
| 2 |
∴S≤46,
即四边形ABCD的面积的最大值是46.
点评:本题考查了矩形性质和判定、勾股定理、根式的计算、完全平方公式等知识点,主要考查学生的理解能力和推理能力,题目综合性比较强,难度偏大.

练习册系列答案
相关题目
 (2012•无锡一模)如图中几何体的俯视图是( )
(2012•无锡一模)如图中几何体的俯视图是( ) (2012•无锡一模)如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连接GF.下列结论 ①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有( )
(2012•无锡一模)如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连接GF.下列结论 ①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有( )