Question

从一张等腰直角三角形纸板中剪一个尽可能大的正方形．应怎么剪，请画图说明你的剪法，如果这张纸板的斜边长为30cm，能剪出最大正方形的面积是多少cm²．

Answer 1

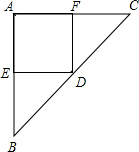
分析：从一张等腰直角三角形纸板中剪一个尽可能大的正方形是以两直角边、斜边中点和直角顶点为正方形四个顶点，设正方形AFDE的边长是a，则AF=DF=DE=AE=a，根据平行线得出△BED∽△BAC，得出比例式，代入求出即可．

解答：解：如图所示：设正方形AFDE的边长是a，则AF=DF=DE=AE=a

这张纸板的斜边BC长为30厘米，则直角边AB=AC=15

2

，
∵四边形AEDF是正方形，
∴DE∥AC，
∴△BED∽△BAC，
∴

DE

AC

=

BE

AB

，
∴

a

15 2

=

15 2 -a

15 2

，
解得：a=

15

2

2

，
∴最大正方形的面积为：（

15

2

2

）²=112.5（cm²）．
故能剪出最大正方形的面积是112.5cm²．

点评：考查了图形的剪拼，本题根据是理解尽可能大的正方形是以两直角边、斜边中点和直角顶点为正方形四个顶点及斜边中线是正方形的对角线．