Question

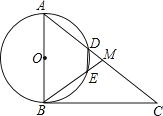
【题目】如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠DCE=90°．

（1）求证：BD=AE；

（2）若△ACB不动，把△DCE绕点C旋转到使点D落在AB边上，如图2所示，问上述结论还成立吗？若成立，给予证明．

Answer 1

【答案】（1）见解析；（2）结论成立．

【解析】

（1）欲证明AE=BD，只要证明△ACE≌△BCD（SAS）即可；
（2）结论成立，证明方法类似（1）.

（1）证明：∵△ABC和△ECD都是等腰直角三角形，

∴CE=CD，CA=CB，∠ACE=∠BCD=90°，

在△ACE和△BCD中，

，

∴△ACE≌△BCD（SAS），

∴AE=BD．

（2）解：结论成立．

理由：∵△ABC和△ECD都是等腰直角三角形，

∴CE=CD，CA=CB，∠ACE=∠BCD=90°，

∴∠ACE=∠BCD，

在△ACE和△BCD中，

，

∴△ACE≌△BCD（SAS），

∴AE=BD．